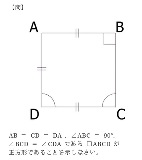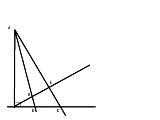
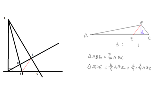
偍偟偊偰両丂偝傫偡偆
[慡偰撉傓]
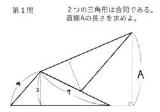
AE:EC=3:1
AD:DB=6:1偺偲偒丄
仮ADE = 仮ABC 亊 3/4 亊 6/7
側傫偰幃傪棫偰偰夝愢偟偰偨傫偩偗偳丄捈妏偱傕側傫偱傕側偄曈偺挿偝
偺斾傪妡偗傞側傫偰丄廗偭偨婰壇偑柍偄丅
嶼悢偺斖埻偺偼偢側傫偩偗偳丄岞幃偺柤慜偲偐傢偐傝傑偡偐丠
| 乧 |
懠偵彂偒朰傟偰偄傞忦審偑偁傞偲偐丠 |
| 乧 |
 晛捠偵乮掙曈亊崅偝亐俀乯偩傠 B傑偱偺崅偝h偑堦掕側傫偩偐傜E偑AC忋偺偳偙偵偁傠偆偑AE:EC偺挿偝偺斾偑柺愊偺斾 |
| 乧 |
偍偍丄側傞傎偳丅 |
| 乧 |
 may偵偁偭偨偐傜偮偄偱偵揬偭偲偔 |
| 乧 |
 弶傔偰搳峞偡傞偺偱彑庤偑傢偐傜偢傕偟幐楃偑偁偭偨傜屼柶傫偝偄丅偨傑偵恊愂偵嫵偊傞掱搙偺抦幆偟偐側偄偺偱偡偑丄彫妛惗偱偟偨傜斾偺栤戣偺墳梡偐偲巚偄傑偡丅憡帡側嶰妏宍傪擇慻扵偟偰斾傪懙偊偰夝偔偺偐偲巚偄傑偟偨丅堦墳夝偄偰傒傑偟偨丅 |
| 乧 |
 杮暥柍偟 |
| 乧 |
慡慠娙扨偵彫妛惗偵愢柧弌棃傑偡傛丅 仮俙俢俤亖仮俙俛俤亊俇乛俈 仮俙俛俤亖仮俙俛俠亊俁乛係偱偡偹 廬偭偰丂仮俙俢俤亖仮俙俛俠亊俁乛係亊俇乛俈偲側傞丅 偍巇晳偄偱偡丅撪偺柡偵柧擔傗傜偣偰傒傑偡丅 |
| 乧 |
彫妛惗偺栤戣偲偼抦傜偢偵恾宍偺僷僞乕儞偐傜偡偖儊僱儔僂僗偲偐偱傗偭偰傒傛偆偲偐巚偄晜偐傋傞偺偼丄偁傞堄枴愭擖娤側傫偩側丅 |
| 乧 |
>>No.108323 偁乕偦偆偄偆偙偲偐丒丒丒丒偁傝偑偲偆丅 偳偆傕曗彆慄堷偔暯柺偺栤戣偼嬯庤偩丅 偙傟偼夝摎偺夝愢偺堦晹側傫偩偑丄偦偺夝愢傑偱昁梫偵側傞偲偼丂orz |
| 乧 |
No.108328偝傫傕偁傝偑偲偆丅 > 仮俙俢俤亖仮俙俛俤亊俇乛俈 偵側傞棟桼偑婥偯偗側偐偭偨傢偗偱偡丅 >>No.108327 偍偋丒丒丒丒偦傫側庤傕丅 嘆嘇偺忦審傪媮傔傞偙偲帺懱偱彫栤偑偱偒偦偆側丅 |