���w���ӂ��Εۊnj� [�߂�]
 8��31���������܂�
8��31���������܂�[
�S�ēǂ�]
���ꂩ��A����N���X�̒��ɏ������W�߂�B
�N���X�̒��ɁA�����a�����̏�����2�l�i�ȏ�j����m����50%�ȏ�ɂ������B
���l�̏������W�߂�������낤���H
23�l
78�l
183�l
365�l
���[�N��o�q�͍l���Ȃ����̂Ƃ���
| �c |
�C�ӂ̌����ɐ��܂��m�����ϓ��Ă̂��������� |
| �c |
(364/365)*(363/365)*�E�E�E*((366-n)/365)<0.5 |
 8��15���������܂�
8��15���������܂�[
�S�ēǂ�]
A person dies, and he arrives at the gate to heaven. There are 3 doors in the heaven. One of the door leads to heaven, second one leads to a 1-day stay at hell and then back to the gate and the third one leads to a 2 day stay at hell and then back to the gate. Every time the person is back at the gate, the 3 doors are reshuffled. How long will it take the person to reach heaven?
| �c |
���̖��͑f���炵��
�Ȃ�قǁI�Ɗ��S����
�������Ώ���
�������H��Ώ��������
�҂��Ă��I�I |
| �c |
�ݖ⒆��"in"�̎g�����Ɉ�a��������Ȃ�
"3 doors in the heaven"�@�Ƃ���̂Ńh�A�͓V���̒��ɂ���
�܂�Q�[�g�̃h�A�ɓ����������_�ł��̐l�͓V���ɂ��邱�ƂɂȂ�
�ݖ�̈Ӑ}�����������\���Ȃ�"in the front of"�� |
| �c |
�ԈႦ��"in front of"��������w |
| �c |
�������݂������l�ɂ���č폜����܂��� |
| �c |
1�^�[�����ɂ��ꂼ��1/3�̊m����0�_�A1�_�A2�_�����_�����Q�[����
1�^�[��������̊��҉��_�ʂ�+1�_
�ŁAn�^�[���܂Ŏ��{��2/3�̊m����n+1�^�[�������邩��A
�@�I���܂ł̊��ғ��_=∑[n=1..��](+1)*(2/3)^n = 1/(1-2/3) = 3 |
| �c |
x = 1/3 * 0 + 1/3 * (1 + x) + 1/3 * (2 + x)
x = 3 |
| �c |
�ȁH
�����Ă��ꂽ����
�������敉���� |
| �c |
���E���z�[�����X�������Ă����̂ł���
�V���ɂ�������Ȃ��ł��傤��
�ꉞ�J�g���b�N�̐���Ă��܂� |
| �c |
�Ⴆ�E���܂��낤��
�s���Ƃ���͓V�������Ȃ��̂ł����S�� |
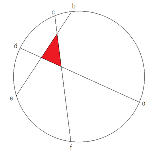 8��17���������܂�
8��17���������܂�[
�S�ēǂ�]
�P�ʉ~�����6�_��}�̂悤�ɐ����Ō���ō����O�p�`�̖ʐ�(�Ԃ�����)���ʒ��̔�ŋ��߂������Ǎ��Z���w�̔��e�łł���H
| �c |
���ׂ��ƘA���������ŏo�������ȋC�������������Ǐo���Ȃ����� |
| �c |
�~�̒��S�����_�ɁA�~����̈�_��(1,0)�֎����Ă���悤�ɍ����ϊ�������
�ʒ��̔䂩��Ίp�A�Ίp����e�_�̍��W�����߂�
���Ƃ͌�_�����߂�̂ɎO�A�������������āA��_�̍��W����O�p�`�̖ʐς��킩��
���̃v���Z�X�ʼn�����Ǝv�����v�Z��... |
| �c |
�Ⴆ���A�X����̓_a,b,d,e�����̂܂܌Œ肵�Ă����āA����cf��P�ʉ~�̒��S�ɂ��ĉ�]������Ɛԓh��̖ʐς͂ǂ��Ȃ�H
���ɂR�̌ʒ��̔䂾���Ŗʐς���ӓI�Ɍ��܂�̂Ȃ�A���ꂼ��̐������~�̒��S�ɑ��ēK�X�ɉ�]�����āA�Ⴆ��b=c,e=d�܂œ������Ă��ꏏ����ˁH |
| �c |
�����ƌ����A
�u�X����̓_a,b,d,e�����̂܂܌Œ肵�Ă����āA����cf��P�ʉ~�̒��S�ɂ��ĉ�]������v
�Ă̂����A�i�Ԃʂ�́j�O�p�`�̂Q�̊p���ς�����Ⴄ��ˁB |
| �c |
���̒�������Ȃ��āA�ʂ̒�������Ȃ��́H |
| �c |
���������Aad,be,cf�̐����䂾�Ɠǂ݈Ⴆ�Ă��B |
| �c |
�ƂȂ�ƁA�ʒ��̔�͈�ʂɂ͂U�̐��̔�ɂȂ��H |
| �c |
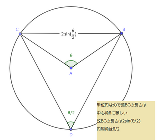
�Ƃ肠������{�I�Ȑ��� |
| �c |
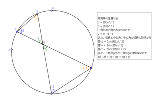
�������������ł������ƌv�Z����Γ������o����������
��ςȂ̂ł܂��o���ĂȂ� |
 ���
8��17���������܂�
���
8��17���������܂�[
�S�ēǂ�]
�N��������������
| �c |
157 ���邢�� 79
��=1 ��=3 ��=4
���������Z�A�c�������Z
�}���͂ނ̂��ݏ�
�ݏ�̏��Ԃ��s���Ȃ̂œ������Q�������B |
| �c |
�����肪�Ƃ��������܂��B
����157�ɂȂ�܂����B |
| �c |
3^1^4 ���ǂ����߂��邩�łQ�ʂ肠�邼�B
(3^1)^4 ���낤�� 3^(1^4) ���낤���B
�������ƕ��ʂ͑O�҂��낤���A�}�`�\�����Ƃ킩��Ȃ���ˁB |
| �c |
���Ɓ���27������3�A�����ėݏ�
a��b��a^b��4������1��4
���Ƃ̓m���� |
 8��16���������܂�
8��16���������܂�[
�S�ēǂ�]
��X���F�m���Ă���F���Ƃ͂��̎��g����ɑ��݂��Ă��邠��Ԃ��_�̘A�Ȃ�ł����Ȃ��̂ł��傤���H
���̐Ԃ��_�ɏ���Ă����X�͉F���͘A�����đ��݂��Ă���Ǝv���Ă��܂������͓_�ł��Ă���̂ł����H
| �c |
�܂��ǂ����Ă����v�����̂��������Ȃ��Ƙb�ɂȂ�� |
| �c |
�������ɋN������z���m�~�[�͂�����Ƃ���ɏo�Ă��邾��
�����ł������ς� |
| �c |
�������݂������l�ɂ���č폜����܂��� |
 8��02���������܂�
8��02���������܂�[
�S�ēǂ�]
���Ȃ��̔]�́A�m�̌���ł͂Ȃ�
�f�[�^�̏������u�ɉ߂��Ȃ�
�]�͌܊��ƌĂ���e���ʂ��ăf�[�^����肱��
�`������Ă���G�l���M�[���A���̂Ɋւ��邱��܂ł̃f�[�^�ɏƂ炵�ĉ��߂���
�]�͂��Ȃ�������m�o��������������̂ł����āA������������������̂ł͂Ȃ�
���̒m�o�����ɁA���Ȃ��͐^����m�����Ǝv�����A���͔��������m��Ȃ�
�{���́A���Ȃ����m��^���́A���Ȃ����n�����Ă���̂�
| �c |
>�{���́A���Ȃ����m��^���́A���Ȃ����n�����Ă���̂�
�����U�肵������n�����������͂̓T�^ |
| �c |
���߉ނ��܂������������̂𒆍��ɓ`����
������R���p�N�g�Ɋ���ɂ����̂�
�F������ |
| �c |
�܁A�W���I�ȏW���_�Ƙ_����p���āA�����鐔�w�I�Ώۂ͋�W������\���ł��邩��ȁB |
| �c |
>��Ō������ĉ��H
��[
�����������ǁA���O�A�r�炷�C���X�Ȃ̂������Č����邩��ȁ[
����Ȃ� |
| �c |
�܊��Ɣ]���Ⴀ�̐���m�o�ł���悤�ɂ͏o���ĂȂ������ |
| �c |
>���͔��������m��Ȃ�
�Ȃ�Ŕ������Ă킩��́H |
 8��06���������܂�
8��06���������܂�[
�S�ēǂ�]
1976�N�ɑ���c��w�̓��w����
�T��ɂP��̊����ŖX�q��Y��邭���̂��鏭�����A�R���̉Ƃ����ԂɖK��ĉƂɋA�����Ƃ��A�X�q��Y��Ă������ƂɋC�������B
�������Q���ڂ̉ƂɖX�q��Y��Ă����m���́H
�@16/125�i��12%�j
�A4/25�i��16%�j
�B20/61�i��32���j
| �c |
>���Z�����x���̖��Ȃ̂ɂ��������������ė������Ȃ��l���N���ċc�_�ɂȂ���
�o��҂��N�Y�����炾�� |
| �c |
No.111982
�N�Y�͂��O���� |
| �c |
��������No.111981���N�Y���������_ |
| �c |
����A�ǂ��l���Ă����O���� |
| �c |
>����A�ǂ��l���Ă����O����
�o�J���ǂ��l�������Č��_�o���Ȃ�����
>�o��҂��N�Y�����炾��
����ɐs����
���_�͋�̓I�ɂȁH���o�J����♡ |
| �c |
>���Z�����x���̖��Ȃ̂ɂ��������������ė������Ȃ��l���N���ċc�_�ɂȂ���
���Z�����x���Ȃ̂ɗ����ł��ĂȂ��l���N���Ă������Ȗ��o���Ă�P�[�X���U������邪�H |
| �c |
����A�ǂ��l���Ă����O����@ |
| �c |
>�����t���m�����č��Z�����x���̖��Ȃ̂ɂ��������������ė������Ȃ��l���N���ċc�_�ɂȂ���
�����A�Z�@�Ƃ��Ă͍��Z�����x�������炻���v���낤����ǁA�m���̈�ʘ_���ƁA�h���ۂ̖��W�h�Ɓh���ۂ̓Ɨ��h�̘_���W����������Ȃ�����A���w�҂ł����v�w�����傾�Ɛ̂͊֘A������Ō���Ă���B
��������A���X�v�������������邵�ˁB |
| �c |
>�u�����v�����ŒP�ɋL�����ł���Έ���������Ȃ��i����Ӗ�����L�����w�o�J�j
�����ɂ��݂��ˁ` |
| �c |
�u�T��ɂP��̊����ŖX�q��Y���v���Ă��������Ȃ���
�u�T��O�o����x�ɂP��̊����ŖX�q��Y���v�̂�
�u�T���K�˂閈�ɂP��̊����ŖX�q��Y���v�̂�
�s�������
�O�҂̏ꍇ�̌v�Z�͂ǂ��Ȃ��i�R�R���H�j |
 8��10���������܂�
8��10���������܂�[
�S�ēǂ�]
������A�ߑO���ɐႪ�~��n�߂��B
��͂˂Ɉ��̃y�[�X�ō~��B
����Ԃ����߁iAM12���j�҂�����ɓ����o���A1���Ԃ�2�}�C���̏�����������A�����1���Ԃ�1�}�C���̏�������������B
��͂��~��n�߂��H
| �c |
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |
| �c |
�˂����݂ǂ��낪�������邯��
��҂̈Ӑ}�����ݎ���đf���ɉ����
�ߑO11�F43������ |
| �c |
��������
���Ȃ݂ɐ�����
�ߑO11��23��
�����ϕ��ΐ�����g��������
���߂���0.618���ԑO�ɐ�͍~��n�߂��B
�Ƃ��������ɂȂ�
�炵�� |
| �c |
��̕t���ǂ��낷��킩��Ȃ�
�A�v���[�`���v���������Ŕ�}���ȁ[�Ǝv�� |
| �c |
>�Ƃ��������ɂȂ�
>�炵��
����͑f���ɕ�����Ȃ���ŃX�����ĂĂ�̂ŔF�߂Ă�� |
| �c |
�ς�n�߂Ă����̐ς��葱����ʂƏ���ł���ʂ��O���t�ɏo���Ȃ����� |
| �c |
����Ԃ����鑬�x�͐ϐ�ʂɔ���Ⴗ����Ă��Ƃ��� |
| �c |
>����Ԃ����鑬�x�͐ϐ�ʂɔ���Ⴗ����Ă��Ƃ���
�����܂ł��炢�Ȃ�o�J�ȃI���ɂ��킩��̂Ńh���炷��� |
| �c |
�Ⴊ�ς����ĂȂ���Ό������鏜��Ԃ�ׂ�������
12�`13���̊Ԃɐi���� = 2*(13�`14���̊Ԃɐi����)
�Ⴊ�~��n�߂Ă���t���Ԍオ13���Ƃ����
log(t)-log(t-1)=2(log(t+1)-log(t))
�v�Z�����t^2-t-1=0
2���������Ƃ��āA13-t�������߂���� |
| �c |
��
�[�I
�G���K���g
�����̂�12�����炾���� |
 �ǖ�
8��07���������܂�
�ǖ�
8��07���������܂�[
�S�ēǂ�]
1�������y�[�W���j�ꂽ�{������B
�j��Ă��Ȃ��y�[�W�ԍ������v�����15000�ɂȂ�B
�j�ꂽ�y�[�W�͉��y�[�W�ڂ��낤���H
��@��
���w���ɂ��[���ł���l��
| �c |
>���ꂷ��N�ɂ͗����ł��܂�����
�͂͂�
�Ȃ�ق� |
| �c |
�\����1�y�[�W�ڂȂ���Ȃ�����B
2�y�[�W�ڂ���1�y�[�W�ڂƃJ�E���g����{�Ȃ̂�? |
| �c |
>2�y�[�W�ڂ���1�y�[�W�ڂƃJ�E���g����{�Ȃ̂�?
�\�P�\�Q�Ƃ��\�\�����\���Ƃ����낢�날���Ő}�����Ă��炦�܂��� |
| �c |
1���̃y�[�W�̍ŏ��̕�����y�[�W�A���̂ق��������y�[�W�Ƃ���B(���ʂ̖{�͂����Ȃ��Ă���)
174�y�[�W�ڂ܂ł̃y�[�W�ԍ���S��������15225�ƂȂ�B
(174+1)x(174/2)=175x87=15225
111�y�[�W�ڂ��j��Ă�����111�y�[�W�ڂ�112�y�[�W�ڂ��Ȃ��Ȃ�̂Ŏc��̃y�[�W�ԍ��𑫂���15002�ƂȂ�B
112�y�[�W�ڂ��j��Ă��Ă�111�y�[�W�ڂ�112�y�[�W�ڂ��Ȃ��Ȃ�̂Ŏc��̃y�[�W�ԍ��𑫂���15002�ƂȂ�B
113�y�[�W�ڂ��j��Ă�����113�y�[�W�ڂ�114�y�[�W�ڂ��Ȃ��Ȃ�̂Ŏc��̃y�[�W�ԍ��𑫂���14998�ƂȂ�B
114�y�[�W�ڂ��j��Ă��Ă�113�y�[�W�ڂ�114�y�[�W�ڂ��Ȃ��Ȃ�̂Ŏc��̃y�[�W�ԍ��𑫂���14998�ƂȂ�B
1�������j��Ďc��̃y�[�W�ԍ��̍��v��15000�ƂȂ���͂Ȃ��B |
| �c |
173�y�[�W�ڂŏI����Ă��̗���174�y�[�W�Ə�����Ă��Ȃ��ق�Ȃ�25�y�[�W�ڂ�26�y�[�W�ڂ���Ԃ�Ă�����15000�ɂȂ邯�ǁA�Ȃ�a������ȁB |
| �c |
>(���ʂ̖{�͂����Ȃ��Ă���)
�����X�����ǂ�������������̂ǂ������Ƃ��������͂Ȃ���
1�y�[�W�ڂ��E�n�܂荶�n�܂�Ƃ���ʂ��Đ��{���͂ǂ����ɂ��Ή����� |
| �c |
����ƃy�[�W�ԍ����\�����ɂ����ė��������{������H |
| �c |
> H - u + u = 1499
�����o�Ă邶��� |
| �c |
�X���b�h�𗧂Ă��l�ɂ���č폜����܂��� |