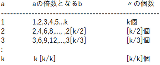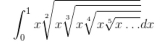
Can y'all solve this

14日13:40頃消えます[全て読む]
Yo what's up I'm an american and I have a little problem for y'all. Who can solve?

これは上記のテキストの翻訳です。 Google翻訳を使用しているので、正しくない可能性があります。 「こんにちは、皆さん、お元気ですか。私はアメリカ人で、皆さん全員が解決することに少し問題があります。あなたのベストショットと、テキサス州ヒューストンの皆さん、こんにちは。」このスレは古いので、もうすぐ消えます。

…	定積分の中の関数 = x^(1/1!) x^(1/2!) x^(1/3!) x^(1/4!) ... = x^(1/1!+1/2!+1/3!+1/4!+...) = x^(e-1) ∫[0,1]x^(e-1)dx = [0,1](x^e /e) = 1/e

13日06:15頃消えます[全て読む]
1からkまでの自然数から重複を許してランダムに二数を選び、それぞれa,bとする。また、k以下の素数の数をpとする。

kまでの自然数が全て同様に1/kの確率で選ばれるとき、b/aおよびa/bの一方もしくは両方が自然数になる確率をk,pで表せ。このスレは古いので、もうすぐ消えます。

…	まずa≦bに限って考える bがaの倍数になる場合の数Dはガウス記号[]を用いてD = k+[k/2]+[k/3]+...+[k/k] (画像参照)a≦bの制約を外した時にa,bが問題の条件を満たす場合の数は 2(D-k)+k = 2D+k なので求める確率はa,bの取りうる場合の数k^2で割ることで (2D+k)/k^2残る問題のD だけどどうやらこれに等しいらしいが…https://en.wikipedia.org/wiki/Divisor_summatory_functionpとkで表示する方法がワカラン

…	最大素数の簡単な見つけ方 ①確認されてる最大の素数と その１個前の素数を掛ける ②それに１足す