
Name名無し22/06/29(水)10:55:21No.117103そうだねx1
23年3月頃消えます[全て読む]
本文無し
| …No.117098+>めちゃくちゃ収束遅そう 収束の速さの具体的な順序は quadratic convergence>linear convergence>logarithmic convergence https://en.wikipedia.org/wiki/Rate_of_convergence linear convergenceが普通の収束でn桁得るための項数はO(n) quadratic convergence以上が速い収束でn桁得るための項数はO(log(n))で済む logarithmic convergenceが遅い収束でn桁得るための項数はO(n^c), c>1あるいはそれよりも大きい 上記の式の収束はlinear convergenceでMachin-like formulaとほぼ同等 quadratic convergenceの例はGauss-Legendre algorithmでlogarithmic convergenceの例はWallis formulaなど |
| …No.117099+書き込みをした人によって削除されました |
| …No.117100+>https://en.wikipedia.org/wiki/Rate_of_convergence エラーの比(μ)が1/4だからnが10増えるごとに6桁ずつ求まる感じかな √かかりまくってるから有効数字かなり要求されそう |
| …No.117101+>√かかりまくってるから有効数字かなり要求されそう 正確には最後の√の中の引き算で桁落ちが起きるので精度が悪くなる https://ja.wikipedia.org/wiki/%E8%AA%A4%E5%B7%AE wikiの通り桁落ちが起きないように修正し (いわゆる分子の有理化を繰り返し)て得られる式はVieteの公式そのものになる https://en.wikipedia.org/wiki/Vi%C3%A8te%27s_formula |
| …No.117102+結局なんのスレだったんだろ |
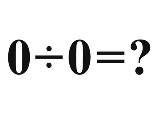
| …No.116974+O |
| …No.116981+とオモタがlog(0)は不定っていやー不定やったな、 |
| …No.116982+m^(n+1) = (m^n)*m よって m^(n+1)÷m = m^n ここで m=n=0 とすると 0÷0 = 0^0 ここで 0^0=1 より 0÷0 = 1 |
| …No.116989そうだねx11 |
| …No.116996+>No.116982 mで両辺を割る前にmが0でないことを確認することを必要だったはず…… |
| …No.116997そうだねx10で割るの禁止というルールは証明可能なことがらでつか 証明不可能なら公理やん |
| …No.117000+0で除算しました(エラー |
| …No.117005+証明できると言っていいかは分からんが 環を局所化する際に積閉集合に0が含まれると 環の構造が潰れて零環になってしまうから 体の構造を持つもので分母に0は置けない |
| …No.117012+補足すると 環の局所化と同型ではない体が存在したとしても 1=0/0=(0+0)/0=2より 1=0となりやはり自明な体となるので 体のような代数構造と零除算は両立できない |
| …No.117097+①数で考えるとa×b=cでa=0のときc=0すなわち0×b=0で これは「いかなるbでも成り立つ」 これをc÷a=bに当てはめると0÷0=「いかなるbでもありうる」 ②ちなみにb=0のときc=0すなわちa×0=0および0÷a=0で これも「基本的には」「いかなるaでも成り立つ」 ③でも②は0÷0=「いかなるbでもありうる」(①)というのと相容れない ④しかし0×b=0がいかなるbでも成り立つことは相変わらず正しい ⑤これら①②③④全てが正しい場合 「このように÷aが÷0すなわち0除算だったときに限り例外的にbの値は定まらなくなる性質があり これは0÷a=bのときb=0になる通常の性質よりも優先される」 ということに結局なる ⑥c÷a=bでa=0かつc=0のときも「÷aの性質が例外的に優先される」ので 0÷0=「いかなるbでもありうる」の妥当性は通常と例外の場合を考慮してもなお保証されている 証明の方針としてはこんなもん…? |
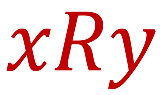
…No.116527そうだねx3  >ヒルベルトの公理主義の内容すら理解しとらんからこういう駄スレを連発するはめになる. |
| …No.116533+キューネンは読むよ 邪魔したね じゃ |
| …No.116537+書き込みをした人によって削除されました |
| …No.116538+アリティーというのかどうか知らんが 「〜が2個以上存在する」という命題を証明する場合の2というの数の基礎付けは どこからやって来るんじゃ…… そいつは証明以前に現れる数なわけだけんども、 それとも思いつく限りの命題(を形式的に表した文)を含む集合が 形式っ的に構成できるから無問題?? としている??? |
| …No.116539+もしそうなのだとしたら 集合論で作った数とペアノ的自然数が区別できないという主張は かなりいかがわしい 後者はこの手のアリティー(?)の処置の仕方を知らん |
| …No.116936+書き込みをした人によって削除されました |
| …No.116937+数学なんてわかりません。 |
| …No.117094+書き込みをした人によって削除されました |
| …No.117095そうだねx1帰ってきたぞおおぉぉぉ そもそも論理学にもいくつかあるということが分かった 初歩的な論理学では初歩的な変数などを並べると論理式になり この初歩的な論理式から順序数としての自然数全体の集合ω omega が作れる これで順序数の連番と対応するラベルとしての記号を作り そうして素朴な論理学と同じ機能を持つフォーマルな論理学その1としての記号論理学を作れる その後記号論理学の論理式で基数としての自然数(個数=有限基数)や自然数全体の集合(aleph0)を作って フォーマルな論理学その2としての「無限個の変数を扱える」モデル理論を作って n変数関数やn項関係も作ってこれで既存の数学を扱い切る そもそもn変数関数やn項関係をモデル理論以前の論理式の仮の記法として考える場合は それらは実は論理式に過ぎず自然数の出てくる余地はない モデル理論でn変数関数やn項関係を「ちゃんと書く」場合 アリティとかの自然数に意味が出てくる とりあえずこんなとこ(キューネン数学基礎論講義第I章)でバテた この話題の本丸の第II章はまた後でゆっくりやったらあああァァァ |
| …No.117096+>「〜が2個以上存在する」という命題を証明する場合の2というの数の基礎付けは >どこからやって来るんじゃ…… 基数としての自然数(個数・有限基数)を使うモデル理論の論理式は 基数としての自然数の定義や記号論理学の論理式の構成が要る だからこれは実はかなり複雑な数学的対象になる >もしそうなのだとしたら >集合論で作った数とペアノ的自然数が区別できないという主張は >かなりいかがわしい 有限順序数としてのペアノ的自然数を構成するには 素朴な論理式は使うが実は「アリティのあるn変数関係やn項関数」は追放しきれる 自然数も自然数全体の集合も順序数(順番)と基数(個数)の話が出てくるが 実は個数は順序数を使っておりしかも順序数よりはるかに複雑な手間が要る 順序数は比較的単純に作れる(とはいえそれなりに大変) そういうことのようです |
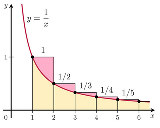
…No.117089+ 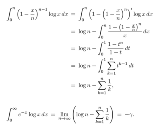 γ=-Γ'(1) |
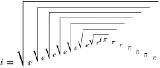
| …No.117034+>No.117031 嘘やないか |
…No.117035そうだねx1  本文無し |
…No.117036+  A217571 |
…No.117037+  本文無し |
…No.117038+  Kill 高橋しょう子 |
…No.117043+  本文無し |
…No.117044+  本文無し |
…No.117053+  本文無し |
…No.117055+  john titor |
…No.117086+  本文無し |
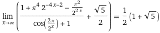
| …No.117081+ Ramanujan's Notebooks IV p353 https://archive.org/details/ramanujans-notebooks/Ramanujan%27s%20Notebooks%20IV/page/n181/mode/2upに載っている黄金比を使うπの公式の高次版1/π = 10(√√5)Σ[n=0,∞] (((2n)!)^3/(64^n(n!)^6))(1+6n((1+√5)/2)^2)((1+√5)/2)^(-24n-8)ラマヌジャンはなぜこの式を載せなかったのだろうか? |

| …No.117078+焼酎:果汁:炭酸水≒1:1:2 |
| …No.117084+まあまあおいしくできました。 |

| …No.117047+Googleが円周率「100兆桁」の計算に成功、世界記録を更新 https://japan.cnet.com/article/35188774/ |
…No.117056そうだねx1  モジュラ関数使ってπの高精度近似式作ってみた 近似1−精度26桁ln(2^21/(√√5-1)^24+24)/10近似2−精度24桁(1695760√(27(2405+308√61)^2-3))/(6741337514+864395093√61)近似3−精度114桁ln((((18+5√13)(15-2√13+√61)(6+√(8+√793)))^12/18^6-24)^2-552)/(2√793)この手の近似式は無数に作れるんだよな |
| …No.117057+>近似2−精度24桁 これはふつうに24桁書けよ |
| …No.117058+>モジュラ関数使ってπの高精度近似式作ってみた > >近似1−精度26桁 >ln(2^21/(√√5-1)^24+24)/10 > >近似2−精度24桁 >(1695760√(27(2405+308√61)^2-3))/(6741337514+864395093√61) > >近似3−精度114桁 >ln((((18+5√13)(15-2√13+√61)(6+√(8+√793)))^12/18^6-24)^2-552)/(2√793) > >この手の近似式は無数に作れるんだよな 数学ド素人だから分からんけどモジュラー関数ってやつすごいな 勉強したくなった |
| …No.117074+>これはふつうに24桁書けよ j-invariant((1+i√16555)/2)によるπの320桁近似 ln(((27(4+√17)^16(1272659166+396488754√17+175423977√53+54313779√901 +(564772430+112064468√17+79752371√53+14865745√901)√((27+4√53)/7))^2 -12)^3+744)^2-393768)/√25228 これは普通に320桁書くより約半分の文字数です。 なおこれより高精度のj-invariantの式はweb電卓の文字数制限を受けます。 |
| …No.117075+>j-invariant((1+i√16555)/2)によるπの320桁近似 j-invariant((1+i√6307)/2)によるπの320桁近似 に訂正 j-invariant((1+i√16555)/2)の方は ln((((27/4)(2+√5)^38((9+√77)/2)^4 (85146847793546+22332012703462√5+6548161920054√77+2990106636079√301 +3956027188782√385+4172398102317√473+2144806628003√1505+911740255281√2365 +(2458331886460+4035724186058√5+955155736684√77+277184956909√301 +158043017566√385+277558487563√473+172022724089√1505+111985306783√2365)√(69+4√301))^2 -12)^3+744)^2-393768)/√66220 で522桁近似、google電卓等で文字数制限に引っかかります |
| [0] [1] [2] [3] [4] [5] |