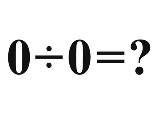
Name名無し22/05/25(水)02:24:25No.116969+
23年1月頃消えます 解いてください

…No.116970+極限なら不定形 自明な体(普通は排除される対象だが)なら0 より一般には未定義

…No.116971+輪だと0/0っていう1つの元になるんだっけ あとスレ画を極限と考えるのは無理な気がする どこにもlimの記号入って無いし

…No.116972+ちなみに輪はクソマイナーな奴でwikipediaで初めて知った https://ja.wikipedia.org/wiki/%E8%BC%AA_(%E6%95%B0%E5%AD%A6)

…No.116973+log(0÷0) = log(0) - log(0) = 0 なので 0÷0 = e^0 = 1、

…No.116974+O

…No.116981+とｵﾓﾀがlog(0)は不定っていやー不定やったな、

…No.116982+m^(n+1) = (m^n)*m よって m^(n+1)÷m = m^n ここで m=n=0 とすると 0÷0 = 0^0 ここで 0^0=1 より 0÷0 = 1

…No.116989そうだねx1１

…No.116996+>No.116982 mで両辺を割る前にmが0でないことを確認することを必要だったはず……

…No.116997そうだねx10で割るの禁止というルールは証明可能なことがらでつか 証明不可能なら公理やん

…No.117000+０で除算しました（エラー

…No.117005+証明できると言っていいかは分からんが 環を局所化する際に積閉集合に0が含まれると 環の構造が潰れて零環になってしまうから 体の構造を持つもので分母に0は置けない

…No.117012+補足すると 環の局所化と同型ではない体が存在したとしても 1=0/0=(0+0)/0=2より 1=0となりやはり自明な体となるので 体のような代数構造と零除算は両立できない

…No.117097+①数で考えるとa×b=cでa=0のときc=0すなわち0×b=0で これは「いかなるbでも成り立つ」 これをc÷a=bに当てはめると0÷0=「いかなるbでもありうる」 ②ちなみにb=0のときc=0すなわちa×0=0および0÷a=0で これも「基本的には」「いかなるaでも成り立つ」 ③でも②は0÷0=「いかなるbでもありうる」（①）というのと相容れない ④しかし0×b=0がいかなるbでも成り立つことは相変わらず正しい ⑤これら①②③④全てが正しい場合 「このように÷aが÷0すなわち0除算だったときに限り例外的にbの値は定まらなくなる性質があり これは0÷a=bのときb=0になる通常の性質よりも優先される」 ということに結局なる ⑥c÷a=bでa=0かつc=0のときも「÷aの性質が例外的に優先される」ので 0÷0=「いかなるbでもありうる」の妥当性は通常と例外の場合を考慮してもなお保証されている 証明の方針としてはこんなもん…？