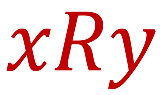
Name名無し22/01/13(木)08:16:42No.116464+
9月20日頃消えます アリティ（n変数関数やn項関係のnにあたる個数）って
どうやって構成するのかよく分からないけどどうやるんだろう
ZFC公理系で自然数や順序数を作る前に
各種公理に∧だの∨だの＝だの出て来るし
これらは2項関係なのでアリティは2だけど
自然数や順序数より前の時点で出てくるアリティは
自然数でも順序数でもないと考えるしかない
じゃあアリティの正体って何なんだろう
構成するためにさらなる道具立てが必要なのか
それとももうこれ以上遡れない原始概念なのか
教えて！　数学板！ 削除された記事が3件あります.見る

…No.116466+個数とやらを仮定します それを使っていろいろやって個数の性質を構成します こうして作った個数が道具として申し分なくなると嬉しいですね これでは困る時はもっと広義の個数や狭義の個数を構成します まあそんな訳で原始概念でも何も問題なくね 集合とやらを仮定してそれを使っていろいろやって 集合の性質を構成するのと同じ（重なるところも多い）

…No.116467+>まあそんな訳で原始概念でも何も問題なくね 集合に帰着しないでいいんだ…？

…No.116502+まあ集合論とかいわゆる数学基礎論ができる20世紀前半まではそんなものが無くても数学は問題なくできあがってたんだよな ただカントールが無限の概念を扱い始めたあたりで数の定義というのをしっかりしとかないといけないと気がつきはじめた

…No.116508+ヒルベルトの公理主義の内容すら理解しとらんからこういう駄スレを連発するはめになる． ヒルベルトが形式主義で非常にシンプルな「証明可能」のメタ理論を考えつく前にラッセルやフレーゲが論理主義の立場から数学の基礎づけ（メタ数学のさきがけ）を行っていた． ゲーデルが不完全性定理を考えているときにも集合論的数学観は主流ではなく，むしろ論理主義の方が先を行っていた． 論理主義は数学を行うには煩雑で面倒な部分もあり，ラッセルらの拘りは数学を大きく制限するものもあったので結局数学を実際に行うためには採用されなかった．

…No.116509+ヒルベルトの方法論はすでにあった形式主義とプラトニズム数学論の折衷案だ． 現象を言葉に起こし，さらに適切に簡略化して記号演算とする形式的ゲームとしての数学の側面と，現実の現象の中に隠れている本質的な概念は人間の存在とは無関係に存在するはずだというプラトン的イデア論を「どっちでもいいじゃないか」と上手いこと混ぜてみせたのがヒルベルトの公理主義だ． アリティの数は例えばポーランド式の形式化で使うが，形式という記号の羅列を「意味づける」外部のメタな理論・定義として存在していればいい． その形式を評価する理論が充分に確証的であることを今日では「有限の立場（確証の立場）」という． 集合論で「数を作った」のではなく，すでに知っていた（と思われる）自然数に対応するそっくりさんを集合論内部でも模倣できるということが重要なんだよ．しかも，そのそっくりさんは”本当に”区別がつかない． つまりペアノ的自然数だけが正義ではないという一例だ．

…No.116527そうだねx3 >ヒルベルトの公理主義の内容すら理解しとらんからこういう駄スレを連発するはめになる．

…No.116533+キューネンは読むよ 邪魔したね じゃ

…No.116537+書き込みをした人によって削除されました

…No.116538+アリティーというのかどうか知らんが 「〜が2個以上存在する」という命題を証明する場合の2というの数の基礎付けは どこからやって来るんじゃ…… そいつは証明以前に現れる数なわけだけんども、 それとも思いつく限りの命題（を形式的に表した文）を含む集合が 形式っ的に構成できるから無問題？？ としている？？？

…No.116539+もしそうなのだとしたら 集合論で作った数とペアノ的自然数が区別できないという主張は かなりいかがわしい 後者はこの手のアリティー（？）の処置の仕方を知らん

…No.116936+書き込みをした人によって削除されました

…No.116937+数学なんてわかりません。

…No.117094+書き込みをした人によって削除されました

…No.117095そうだねx1帰ってきたぞおおぉぉぉ そもそも論理学にもいくつかあるということが分かった 初歩的な論理学では初歩的な変数などを並べると論理式になり この初歩的な論理式から順序数としての自然数全体の集合ω omega が作れる これで順序数の連番と対応するラベルとしての記号を作り そうして素朴な論理学と同じ機能を持つフォーマルな論理学その1としての記号論理学を作れる その後記号論理学の論理式で基数としての自然数（個数=有限基数）や自然数全体の集合（aleph0）を作って フォーマルな論理学その2としての「無限個の変数を扱える」モデル理論を作って n変数関数やn項関係も作ってこれで既存の数学を扱い切る そもそもn変数関数やn項関係をモデル理論以前の論理式の仮の記法として考える場合は それらは実は論理式に過ぎず自然数の出てくる余地はない モデル理論でn変数関数やn項関係を「ちゃんと書く」場合 アリティとかの自然数に意味が出てくる とりあえずこんなとこ（キューネン数学基礎論講義第I章）でバテた この話題の本丸の第II章はまた後でゆっくりやったらあああァァァ

…No.117096+>「〜が2個以上存在する」という命題を証明する場合の2というの数の基礎付けは >どこからやって来るんじゃ…… 基数としての自然数（個数・有限基数）を使うモデル理論の論理式は 基数としての自然数の定義や記号論理学の論理式の構成が要る だからこれは実はかなり複雑な数学的対象になる >もしそうなのだとしたら >集合論で作った数とペアノ的自然数が区別できないという主張は >かなりいかがわしい 有限順序数としてのペアノ的自然数を構成するには 素朴な論理式は使うが実は「アリティのあるn変数関係やn項関数」は追放しきれる 自然数も自然数全体の集合も順序数（順番）と基数（個数）の話が出てくるが 実は個数は順序数を使っておりしかも順序数よりはるかに複雑な手間が要る 順序数は比較的単純に作れる（とはいえそれなりに大変） そういうことのようです