Name名無し21/01/02(土)05:54:37No.114743+
21年10月頃消えます[全て読む]
コレわかりますか？

Name名無し20/12/22(火)23:00:51No.114696+
21年10月頃消えます[全て読む]
激ムズ

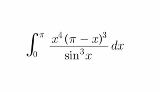
…No.114699+https://ja.wolframalpha.com/input/?i=%E2%88%AB%5B0%2C%CF%80%5D+x%5E4*%28%CF%80-x%29%5E3%2Fsin%28x%29%5E3+dx

…No.114700+Wolfram先生でも数値計算しかしてくれないという…ｗ

…No.114701+9π/8 * (56 π^2 ζ(3) - 62 (10 + π^2) ζ(5) + 635 ζ(7))

…No.114702そうだねx1留数定理を使え、と言われてるだけの問題だよ

…No.114706+>留数定理を使え、と言われてるだけの問題だよ 積分経路どう取るのさ

…No.114707+ 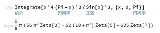No.114701はwolframの計算結果やね

…No.114708+＞全く関係なさそう xが一つ消せるやん そうすればx=π/2で対称だから0→π/2の積分範囲になって… やっぱ解らん

…No.114715+King propertyしてから二項定理で展開すれば、x^n/(sin x)^3を[0,π]で求めればよくて、それは半径1の半円形の積分路を考えることにより、x^2(log x)^n/(1-x^2)^3を[-1,1]で求めることに帰着する、あとはt=x^2と置換してベータ関数の高階偏微分やるだけか

…No.114716+>x^n/(sin x)^3を[0,π]で求めればよくて 発散しない？

…No.114742+>発散しない？ おっと、二項定理で展開できないのか、それなら展開せずにそのまま積分路変更するのが良さそうかな

シストレの途中経過Nameしみじみ20/09/05(土)08:02:23No.114446そうだねx1
21年6月頃消えます[全て読む]
オアンダの結果1

…No.114711+ 結果1

…No.114712+ 結果2

…No.114734+ 結果1

…No.114735+ 結果2

…No.114736+ 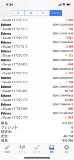結果3

…No.114737+ 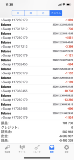結果4

…No.114738+ 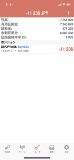結果1

…No.114739+ 結果2

…No.114740+ 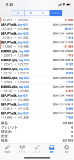結果3

…No.114741+ 結果4

Name名無し20/07/10(金)10:24:47No.114230+
4月21日頃消えます[全て読む]
>子供のころ、こういう天秤を作ったらどっちに傾くのかずっと疑問だった

面白そうなんだが、正直意味がわからん
その後の流れもわからん
みんな何の話をしてるの？
直感的に左に下がると思ったのだが
そうでないなら不思議なんで理由が知りたい
左に下がるなら、直感通りでそれがどうしたとしか思えない

言い方がおかしいな。
こんな形の天秤が公案の対象になる肝を教えてください

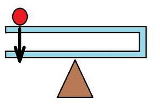
…No.114441+永久機関ができるな

…No.114454+ 涼しげなデッキチェア

…No.114455+キチガイが一人でずっと話題そらそうと必死

…No.114456+>こんな形の天秤が公案の対象になる肝 だろ？

…No.114463+ 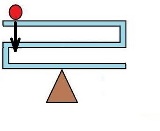これだと・・・

…No.114464+ 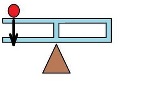これだと・・・

…No.114470そうだねx1 もう、いっそこれで

…No.114725+初心に戻って実験してみれば良いんだ

…No.114726+ﾋｴｯ…、、観察や統計の結果は板チ、、

…No.114732+おそらく右が下がると思い込んでて、間違いに気づいたからおかしなこと言ってごまかそうとしてるのだろう

Name名無し20/12/29(火)00:21:29No.114720+
21年10月頃消えます[全て読む]
整数解(x,y)

…No.114721そうだねx1書き込みをした人によって削除されました

…No.114727+(-1,±1)しか思いつかない

…No.114728+プログラムで-10<=x<=10の範囲で探すと [(-1,-1),(-1,1),(0,-1),(0,1),(3,-11),(3,11)] が見つかった

…No.114729そうだねx2(2x^2+x)^2 = 4x^4 + 4x^3 + x^2 < 4x^4 + 4x^3 + 4x^2 + 4x + 4 = 4y^2 < 4x^4 + 4x^3 + 5x^2 + 2x + 1 = (2x^2+x+1)^2 (|x| > 3) だから、x を整数とすると, |x| > 3 では 2y は整数になり得ない よって整数解は [(-1,-1),(-1,1),(0,-1),(0,1),(3,-11),(3,11)] だけ

…No.114730+ちょっプログラムの実行結果が証明扱いなのですか？！

…No.114731+>ちょっプログラムの実行結果が証明扱いなのですか？！ -3<=x<=3の範囲で代入すればわかることでしょ

クエスチョンName名無し20/12/27(日)19:46:12No.114717+
21年10月頃消えます[全て読む]
本文無し

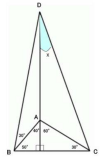
…No.114718そうだねx2tanに関する恒等式 tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) に10°を入れて計算すると tan(3×10°)=tan10°×tan(60°-10°)×tan(60°+10°) tan30°=tan10°×tan50°×tan70° 1/tan70°=tan10°×tan50°×(1/tan30°) tan20°=tan10°×tan50°×tan60° また図より tan(x)=tan10°×tan50°×tan60° となるので x=20° 幾何的な解法は他に委ねる

…No.114719そうだねx2 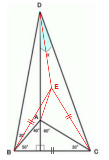（細かい角度計算は省略） △BCEが正三角形となるような点Eをとる。CAは△ABCの対称軸なので∠BEA＝∠EBA＝10°∠BDA＝10°＝∠BEAなので四角形BAEDは円に内接する。したがって∠BDE＝180°−∠BAE＝20°∠DBE＝20°＝∠BDEよりEB＝EDよって△ECDはEC＝EDの二等辺三角形となるので他の角から∠EDC＝10°と計算できる。以上より、x＝∠ADE＋∠EDC＝20°

…No.114722+ 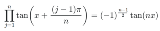>tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) これ一般化するとこうなるらしい

…No.114723+>CAは△ABCの対称軸なので∠BEA＝∠EBA＝10° 訂正：△ABC→△EBC

Name名無し20/11/01(日)19:33:13No.114579そうだねx1
21年8月頃消えます[全て読む]
2つの立方体を合わせた立体があります。
1匹のアリが立体の頂点Aを出発して、表面だけを歩きます。
アリがたどり着くのに一番遠い点はどこでしょうか。

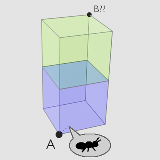
…No.114581そうだねx2正方形の一辺の長さを a 頂点Aを原点 正方形の辺の方向に沿って x軸(右方向),y軸(奥方向),z軸(上方向)とすると (3a/4, 3a/4, 2a)の位置

…No.114582+どうやら頂点ではないと！？ 面白いね 19へぇー

…No.114583+表面だけで考えたいから展開図が欲しいな・・・

…No.114584そうだねx2 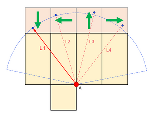目的の点は上面のどこか 展開図上で考えると上面のとり方は4パターンあり、それぞれに対応する最短距離の候補がL1〜L4の4つあるmin(L1,L2,L3,L4)を最大値にするような点が求める点B

…No.114598+この問題は最短距離が最大となる点を答えよという意味？ 遠くするだけなら同じところを任意回ぐるぐる回れば良いわけやし…

…No.114599+展開図上の直線は 実際の立体表面の測地線に必ずなる んでしたっけ…

…No.114714そうだねx1 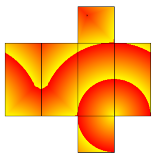分かりやすそうなサイトがあった http://www.se16.info/js/cuboid.htm

Name名無し20/11/23(月)23:43:50No.114631+
21年9月頃消えます[全て読む]
本文無し

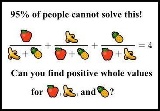
…No.114632+思わずググっちゃったけどエライ問題だなこれ

…No.114633+逆に5%も解ける母集団ってどこだよ

…No.114634+95%って英語圏の決り文句なのか、ぐぐると色々でてくるな 単に多くの人は〜みたいな意味合いだろ

…No.114635+95%ってのは、統計学の信頼区間から来ているんだろ？

…No.114694+数学五輪の過去問や！

…No.114703+書き込みをした人によって削除されました

…No.114704+リンゴっぽいのが女性自身 バナナとパイナップルっぽいのが男性自身 交尾しない分子 交尾した分母 交尾しても1つしか増えないので解は４

…No.114705+メスは多くのオスと交尾しても生まれる子は１

…No.114713+>数学五輪の過去問や！ 数オリでもこんなの出しちゃダメだと思う

Name名無し20/06/06(土)23:22:51No.114123+
3月19日頃消えます[全て読む]
相対性理論についての質問です
１０光年離れた星に、光速の宇宙船に乗って向かう時
かかる時間は１０年
と思ってましたが
宇宙船の中の人にとっては、時間がゆっくり進むので、もっと早く着くことに気付きました。
気付きましたが、なら中の人にとって、どれぐらいの時間で着くのでしょうか？

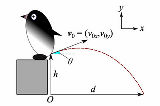
…No.114490+光速30万km/sを9.8m/s2で割って約3000万秒≒1年かかる と見せかけて、光速に近づくと船内時間がゆっくりになる分 1Gを維持するために実加速度も減らさないといけなくなり、永遠に光速に到達できない

…No.114510+光速で移動すると中の人の時間は止まるだろう。アメリカ映画に時々出てくるだろう。

…No.114514+速度が光速に近づくにつれ、宇宙船の質量が増大し・・・・ あ、いやなんでもない

…No.114527+光速で移動すると外の人の時間はめちゃくちゃ速くなるの？ それとも遅くなるの？

…No.114548+書き込みをした人によって削除されました

…No.114553+>光速に達するまで１Gに体が耐えられますか？ 生まれてこのかた1Gの重力に耐えていますが

…No.114562+この人等価原理信じてるよ

…No.114692+人体の反射神経 体内の神経を伝達する信号は、光速の何％ぐらいの速度なんだろうか

…No.114693+↓下記のサイトによると光速の300万分の1らしい。 http://www.infonet.co.jp/ueyama/ip/episode/nervous_system.html

…No.114695+ありがとう

Name名無し20/07/08(水)12:04:22No.114228そうだねx1
4月19日頃消えます[全て読む]
ペンギンは1.34メートル先までウンチを射出できると判明

…No.114301+鳥のオシッコを調べてからウンチの話をした方がいいと思う

…No.114327+総排出口から糞尿も卵も一緒くた

…No.114443+オレは男だが、若くて可愛い女のゲリ下痢ウンチを食べたいね。 ハッキリ言って！！

…No.114445+https://youtu.be/7sG2dZ9UCts?t=124

…No.114691+書き込みをした人によって削除されました