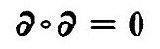Name名無し20/06/15(月)02:33:38No.114161+
3月27日頃消えます[全て読む]
鞍点集合とその近傍の魅力

…No.114167+極小値だと思ったら残念ってなるの嫌い

…No.114224+鞍が発明される前は何と呼ばれていたのだろうか

…No.114225+鞍は紀元前からあるし、ギリシャローマ時代にも伝わっていた

…No.114247+分水嶺みわけ

…No.114408+二次元が三次元になったとたんにこういう厄介な点が出て来るわけだけど四次元以上になったらもっと複雑な状況が起こるんだろうか

…No.114414+>二次元が三次元になったとたんにこういう厄介な点が出て来るわけだけど四次元以上になったらもっと複雑な状況が起こるんだろうか むしろ低次元トポロジーの難問が二次元三次元に集中してるイメージ 無限次元は簡単になるケースがほとんど

AV女優は中国人である。Name佐藤匠20/08/02(日)10:51:00No.114373+
21年5月頃消えます[全て読む]
https://www.shonenjump.com/j/rensai/fulldrive.html

https://oeis.org/A217571

…No.114375+中国語の部屋

…No.114378+可愛的女孩

…No.114379+中国剰余定理

数学の超難問「ＡＢＣ予想」は証明されたかName名無し20/07/16(木)23:02:07No.114297+
4月28日頃消えます[全て読む]
京大・望月教授の論文掲載へ、理解できるのは世界で１０人？
京都大は４月、同大数理解析研究所（数理研）の望月新一（もちづき・しんいち）教授が、長らく未解決だった数学の超難問「ＡＢＣ予想」を証明したと発表した。数理研が編集する国際専門誌「ＰＲＩＭＳ」に掲載する。予想は今後新たな「定理」として生まれ変わるが、海外の研究者からは批判も出ており、論戦が活発化しつつある。望月氏の論文は独創的な理論を駆使しており、世界でも内容を理解できているのは１０人程度とされる。（共同通信＝浅見英一）

ＮＨＫＡＭラジオで17時30分頃から今日（終わった）と明日、解説をしてくれています。
よかったら聞いてみてください

…No.114298+たがいに素の関係の場合で 自然数Ａ（素数）のべき乗、Ｂ（素数）のべき乗だと 数式が成り立つ感じで無限いけそうなんですが 成り立つ数が有限になるとのこと・・・意味がわかりません

…No.114309+じゃ、らじるらじるでき聞いてみるか NHK第一なら聞き逃しサービスがあるな

…No.114310+やっていないじゃないかｗ ガセネタすぎる

…No.114318+ゴジだっちゃ 数学の難問に挑む です

…No.114319+仙台ローカルかよｗ https://www.nhk.or.jp/radio/ondemand/detail.html?p=2914_01 ↑これだな。

…No.114340+後半ね 「数学の難問に挑む（後編）」 https://www.nhk.or.jp/radio/player/ondemand.html?p=2914_01_40042

…No.114369+独創的過ぎてまるで解らん 何言ってるのかね？この教授は

Name名無し20/07/23(木)21:35:03No.114351+
21年5月頃消えます[全て読む]
本文無し

…No.114352+ネコはいます

…No.114353+567を二回かけると321489になって0以外の数字が全て現れるの面白い

…No.114354+それと似たような数って他にもあるのかな

…No.114355+書き込みをした人によって削除されました

…No.114356そうだねx1>No.114354 コンピュータの力を借りて計算した所, 二乗で1〜9が1回ずつ出現する数は 567^2=321489 854^2=729316 のみ 二乗で0〜9が1回ずつ出現する数や 二乗で1,3〜9が1回ずつ出現(2は二乗の表記に使うとして除外)する数, 二乗で0,1,3〜9が1回ずつ出現する数は存在しなかった

Name名無し20/07/14(火)18:56:15No.114271+ 4月26日頃消えます[全て読む]
紙の上に線が交わらないように一周ぐるっと輪になる図形かけば、どんな図形でもその線上で、結べば長方形となるような4点が必ずありそう？

…No.114272+何か反例がありそう 双曲線と円弧を組みあわせるとか

…No.114275+>No.114272 円弧の方に2点ずつ取れば長方形できそうじゃない？ 双曲線の方でもいいけど

…No.114276+書き込みをした人によって削除されました

…No.114277+書き込みをした人によって削除されました

…No.114278+三日月型は？ 斜めに引き伸ばして左右反転の対称性をちょっと崩せば、 周上にとった2点を結ぶ線分の両端から 反対側の周に向かって下ろした足と周の交点2点を結ぶ線分が ぜってー平行にならないようにできそう

…No.114302+ 検証不足な主張が含まれているので証明とはいかないけど考察してみた 点A,Bとこの2点を繋ぐ互いに交わらない経路p1,p2があるこの経路上を互いの距離を一定に維持したまま動く点P,Qを考え,PQの中点が取る軌跡を考える点Aを出発する点をP,点Bを目指す点をQとする点Pが経路p1,点Qが経路p2を通る場合の軌跡(緑)と点Pが経路p2,点Qが経路p1を通る場合の軌跡(桃)について,これらが途切れずに引ききることが可能ならばこの2本は共有点を持つこの共有点を中心としPQを直径とする円 と 経路p1,p2 が交わる点を頂点に選ぶと長方形を作ることができる緑,桃が途切れる場合はPQの距離を変えるか点A,Bの位置を選び直すことによって条件にそぐう問題に帰着することができる

…No.114304+>No.114302 何となくわかる気がする。 ただ緑と青？(桃)の軌跡がどんな感じで動いたのか若干理解できなかった。 あとPとQは経路上の距離じゃなくて平面上の距離であってる？

…No.114311+ >No.114304 あってる点Pが経路p1,点Qが経路p2を通る場合の軌跡(L12,水)と点Pが経路p2,点Qが経路p1を通る場合の軌跡(L21,緑)の他に点P,点Qが経路p1を通る場合の軌跡(L11,橙)と点P,点Qが経路p2を通る場合の軌跡(L22,紫)を追加するとイメージがつかみやすいかも>No.114302は軌跡の色を途中で変更した際に文面上での更新を忘れた惑わせてすまない

…No.114313+>No.114311 なるほど じゃあ後はこれの正統性を示せればええわけや。 図形に対して二つの経路は取れると思うから、なぜ図形と円が交わるような中心ができるのかと、その円との交点で必ず長方形になることさえ言えればええんやな

Name名無し20/07/03(金)17:51:22No.114201+
4月14日頃消えます[全て読む]
わからん

…No.114202+与えられた課題は丸投げせずに自分でやるように

…No.114203+了解です！

Name名無し20/06/26(金)02:54:44No.114178+
4月07日頃消えます[全て読む]
本文無し

…No.114180+たのしいようちえん

…No.114182+ここまでは早熟なのを求めようとは思わんが 小学生でLispやHaskell弄ってるぐらいなら居ても悪くはなかろう

…No.114183+簡単なLispなら小学生のとき覚えたけど Haskellは難しそう

…No.114184+俺自身マシン語使える小学生では一応あったので 現代的にはラムダ式で無名関数さらっと書ける子供が居てくれた方が頼もしい

Name名無し20/04/20(月)06:33:23No.113945+
1月30日頃消えます[全て読む]
安野光雅

…No.114116+「数学をつくった人びと」見たらだいたいおk

…No.114117+ なんとなく貼っておく

…No.114118+微分形式の幾何学的意味： df=∂f/∂x dx + ∂f/∂y dy として ライプニッツの解釈　dx ,dy は無限小の変位 コーシー　εδ法を発明。無限小なんて曖昧な概念は不要！ 当時の数学者はコーシーの画期的証明を見て「dfで散々理論構築しちゃったしなー。そうだ dx,dy,dfを (x,f(x))を新たに原点として捉えた座標軸とすれば、df=∂f/∂x dx + ∂f/∂y dy は接線の方程式と考えることができる！」 シュヴァレーは接ベクトルで定義している

…No.114119+ε-δ論法はワイエルシュトラスが完成させた んだったと思った！

…No.114120+ 本文無し

…No.114121+おっと、１変数の時は接線だけど、２変数の時は接平面だな。

…No.114122+ 本文無し

…No.114133+庵野秀明のエヴァンゲリオンよか 福音館書店から安野光雅のほうが ジブリの品性に近そう

…No.114135+ 本文無し

…No.114147+ >なんとなく貼っておく この本の表題の「形式」って微分形式「機能」って関数とダブルミーニングなんだろうか？まあ深谷先生推薦のアーノルドよりかは解析力学の教科書として親切に思えるが

Name名無し20/05/06(水)02:32:46No.114024+
2月15日頃消えます[全て読む]
コロナで暇だから和算の問題作りまくった
3/4円の中に同じ大きさの大円3つと小円1つ
小円の半径を1としたとき，3/4円の半径は？

…No.114026+ 正六角形の中に辺の長さを半径とする1/3円 正六角形の2辺と1/3円に接する大円2つ正六角形の2辺と大円2つに接する小円これら3つの円と1/3円に外接する楕円の離心率は？

…No.114027+ 正六角形の中に大円12個，楕円，小円4個 小円の半径を1としたとき，正六角形の1辺の長さは？

…No.114028+ 中心角θの扇形の中に同じ大きさの半円2つ 半円が重なったところに同じ大きさの円3つcosθ= 3/4，円の半径を1としたとき，扇形の半径は？

…No.114029+やり出すと詰将棋のように時間をかけてしまうので 最初のだけ。

…No.114030+４√２＋６

…No.114031+離心率って習った記憶がない。 天文雑誌では見るけど。

…No.114032+今作る場合、和算問題と数学問題の違いって何なの?

…No.114033+和算は図のような初等幾何の長さや面積、体積を求める問題が多いんじゃないの？ 「証明」は三平方以外興味の範疇外だったみたい。 後期になると、ネタを西洋の惑星軌道などから求めるようになった。 でも、もっぱら近似計算が認められていたからなあ。 微積が無いから、錐体の体積は柱体の体積の1/2.96なんて独自の数値を使っていた。

…No.114089+こういう問題ばっかり解いていると そのうち最密充填問題の上界を下げ始めるのではな いか

…No.114113+ 三つの円は単位円とする 図のように座標付けする直線y＝x+1+√2放物線y＝x^2/4の交点が正方形の角Aとなる(辺と半径の比率は約０.806らしい)

なんか変な感じName名無し20/05/28(木)04:41:13No.114108+
3月09日頃消えます[全て読む]
Ａ＝Ｂ、Ｃ＝Ｄ
Ａ＋Ｃ＝Ｂ＋Ｄですよね

ポケ＝ポケット、モン＝モンスター
ポケモン＝ポケットモンスター
でも
ポケ盛　＝　ポケット盛　になりません

どんな式を書けば正しいポケ盛になりますか？

…No.114109+>ポケ盛　＝　ポケット盛　になりません ポケ盛のポケは「ポケット」ではなく「ポケモン」を表すものだから

…No.114112+そういやstring の連結演算子で+じゃなくて*が定義されてたのがあったな 順番に意味があるからだとか