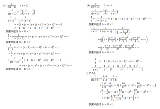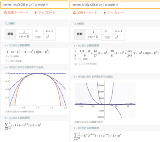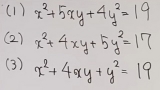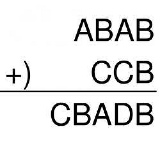
Name名無し20/10/31(土)23:50:39No.114574+
21年8月頃消えます[全て読む]
本文無し

…No.114575そうだねx4答えなし！ 和の最上位桁Ｃが１なのは明らか。 そうすると、加えられる数の最上位桁のＡは９でなければならない。（それ以下だと繰り上がりが発生しない） すると百の位のＢが８しかありえない。（それ以下だと繰り上がりが発生しない） 百の位を考えると、８＋１＝９になって良さそうだが、それだと繰り上がりが発生せず、十の位の和の繰り上がりがあるはずだが、そうなると８＋９＋１＝１０となって、百の位が０になるからＡ＝０となって矛盾

…No.114576+条件を緩和して先頭の桁に0がくる事と違う文字に同じ数字を入れる事を認許すとやっと A=B=C=D=0 が解になる 10進法以外で考えた場合も同様

…No.114577+D=-170とするのはダメなのかい？

…No.114580+どこかのBを13に分解して…という手を考えたけど無理だった

…No.114600+一部界隈で正答率100%の問題だった…

…No.114601+ギンガマンかよ

…No.114604そうだねx2ガンガン　ギギン　ギンガマン　か 懐かし

…No.114678+ロマンチック　止・め・て

Name名無し20/12/06(日)10:10:00No.114671+
21年9月頃消えます[全て読む]
「y=x^(2n) (n→∞）」
のグラフを数学的に正しく表記するにはどうすればよいか
画像はwindows10の電卓による
y=x^1000
のグラフ
ついでに「y=x^(2n)」を上付き文字で表示する方法を教えてください
いろいろ試したけどうまくいかない・・

…No.114672+電卓のアプリは数値計算できないからなのでは？ そういうのは WolframAlfa でやらせようぜ…と思ったが3Dのグラフが出るな

…No.114673+数値計算じゃなく、式計算ね

…No.114674+y = x²ⁿ

…No.114675+↑記述方法をご教示いただきたく

…No.114676+>No.114675 https://en.wikipedia.org/wiki/Unicode_subscripts_and_superscripts

Name名無し20/11/29(日)22:37:54No.114644+
21年9月頃消えます[全て読む]
ここに3つの箱があります。
ある箱にはリンゴだけ、別の箱にはミカンだけ、さらに別の箱にはリンゴとミカンの両方が入っています。
箱には中身を示すラベルが貼ってありますが、どれも正しくないとのことです。
どれか1つの箱から1つだけ果物を取り出して見て、3つの箱の中身を正しく当てることができるでしょうか。

…No.114651+>どれか1つの箱から1つだけ果物を取り出して見て、 たまたま2つの果物が両方入っている箱に行き当たったらどうするんじゃ……

…No.114652+>たまたま2つの果物が両方入っている箱に行き当たったら ・あからさまに他より重いので持ったらわかる ・箱開けなくても振ったらわかる

…No.114653+書き込みをした人によって削除されました

…No.114654+>・あからさまに他より重いので持ったらわかる >・箱開けなくても振ったらわかる 問題文のどこにも「箱に絵の果物が1個ずつ入っている」とは書いていない 箱詰めになっていたらそれでは分からない

…No.114662+実は問題無い？ リンゴ＋ミカン、のラベルの箱から1個果物を取り出した結果がリンゴだったら、 元の箱の中身はリンゴ1個でしか有り得ぬ、 同じく、ミカンだった場合はミカン1個でしか有り得ない

…No.114663+背理背理フレ背理ほー

…No.114664+組み合わせが具体的に列挙可能なサイズの有限集合だから 別に背理法でも誰も文句は言わないはず…

…No.114665+書き込みをした人によって削除されました

…No.114666+書き込みをした人によって削除されました

…No.114667+書き込みをした人によって削除されました

Name名無し20/11/12(木)00:36:52No.114611+
21年8月頃消えます[全て読む]
本文無し

…No.114612そうだねx3（10+20+24）÷2=27kg

…No.114613+下の白い四角も含めろよ

…No.114614+三角の上に丸が乗るのはバランス的におかしいから浮いているのでは ▲=20kg、■=4kg、●=6kgで？=30kg

…No.114619+>三角の上に丸が乗るのはバランス的におかしいから浮いているのでは 上から見てるのでは？

…No.114620+>下の白い四角も含めろよ 左側の線と数字や文字や記号を入れないの、おかしくないですかぁ？

…No.114630+重量ではなくて質量を問題にしているだけかもしれん

…No.114638そうだねx2〇3 △17 □7

…No.114643そうだねx1大きさを見たところそんな大きな重量差があるとは思えない。 どこかに間違いがある。

Name名無し20/07/12(日)10:04:04No.114248+
4月23日頃消えます[全て読む]
イスラエルのスタートアップ企業が、独自の3Dプリンターと食用インクを使って植物由来のステーキ肉を開発したんや。
試食したシェフは、「10人中8人は見分けがつかないだろう」と感想を述べたというんや。
https://www.youtube.com/watch?v=fLpeeUYtW94&feature=emb_title

という記事を見て思った
見分けがつく2人を10人集めたら、全員見分けがつく
ってことなんだろうか？

…No.114252+イスラエルの食肉は血抜きしていないのか?

…No.114253+書き込みをした人によって削除されました

…No.114254+もみぞうのオカルトＵＭＡ板に何年も延々一人でスレ立て続けてるキチガイのスレをなぜ引用するのかね UMA関係なく気になった記事を「なんや」と関西弁風にして転載し続けてる。スレ文もなにがUMAなんだか

…No.114255+ははははは 同好の士がおる（ｗ

…No.114357+とうとう伝説の合成ビフテキが現実に！ え、もうとっくに整形肉が市場を席捲してましたかそうですか

…No.114521+疑問から馬鹿が滲んでるぞ

…No.114621+今度は人間の細胞を培養して作る人肉ステーキが開発されたとのこと。 いったい未来はどうなってしまうのやら。 http://karapaia.com/archives/52296573.html

…No.114625+アンブロシアプラス

…No.114636そうだねx1その10人は無作為に選んだものとするんじゃないの？

…No.114637+似たようなシェフが10人居て見分けがつけにくいという可能性、

Name名無し20/10/18(日)16:51:36No.114536+
21年7月頃消えます[全て読む]
消さないとコロナウィルスで人類が絶滅する。

…No.114609+書き込みをした人によって削除されました

…No.114610+Name名無し 20/11/10(火)19:56:48No.114609+ 書き込みをした人によって削除されました

Name名無し20/11/04(水)15:32:08No.114586+
21年8月頃消えます[全て読む]
解き方教えて

…No.114588+もとの4桁の数をNとする。(1000 <= N <= 9999) Nの各位の数字を合計した数字をxとする。(1+0+0+0 <= x <= 9+9+9+9 つまり 1 <= x <= 36) 例えばx=10の場合、N=x^3=1000でないといけないが、Nの各位を合計しても10にならない。 x=11の場合、N=x^3=1331でないといけないが、Nの各位を合計しても11にならない。 こんな感じで虱潰しに調べていくのでは。

…No.114590そうだねx1自然数 a の各桁の和を S(a)、ある4桁の整数 x と2以上の整数 n を用いて {S(x)}^n = x …(1) が成立するとする n≠2　…(2)なぜならば(1)より x = {S(x)}^2 ≦ 36^2 < 1999 となるので S(x) ≦ S(1999) = 28 再び(1)を用いると x = {S(x)}^2 ≦ 28^2 < 1000 となって x が4桁であることに矛盾 S(x)が3の倍数ならばS(x)は9の倍数…(3)　なぜならば(1)より S(x) が3の倍数ならば右辺 x が9の倍数となるので倍数判定法から S(x) も9の倍数 x, 及び S(x)の一の位は0ではない…(4)　なぜならば S(x) の一の位が0であれば (1),(2) より x は 10^3 を因数に含むこととなり、x が4桁の整数であることと合わせると S(x)<10 となり矛盾 逆に S(x) の一の位が0でなければ(1)の左辺は2あるいは5の因数を含まないので右辺 x の一の位も0にならない S(x)≠2,4,5…(5)　詳しくは省略するが(4)及び2,4,5の倍数判定法から適合する数がないことがすぐに導ける (1)〜(5)を踏まえて可能性が残る(n,S(x))の組は (3,11)(3,13)(3,14)(3,16)(3,17)(3,18)(3,19)(4,7)(4,8)(4,9) あとは個々計算して調べると(3,17)(3,18)(4,7)が適合するので答えは 17^3=4913, 18^3=5832, 7^4=2401

…No.114591+ ありがとうございます この問題も解いてください

…No.114592+とりあえず最初と最後の数字が1と2になりそうな気がする

…No.114593そうだねx21番目だけを空けて残りを4つずつの塊にする 5番目だけを空けて残りを4つずつの塊にする 9番目だけを空けて残りを4つずつの塊にする 13番目だけを空けて残りを4つずつの塊にする 17番目だけを空けて残りを4つずつの塊にする の5パターンを考えると4つの組が100以上でそれぞれ別の正整数が入る事から17個の整数の総和の最小値が405以上である事はわかる 総和が405になるパターンは数の選び方並べ方によって複数あるが　例えば次の通り なお4つずつで改行を入れながら考えると作り易いと思ったのであえて改行をそのまま残している 1,30,31,38, 2,29,32,37, 3,28,33,36, 4,27,34,35, 5

…No.114602+ ありがとうございます この問題も解いてください

…No.114603そうだねx1(1)2の倍数は21個 偶数1つあたり7個の2の倍数が作れるので、偶数は3つある ⇒取り除いたのは偶数 (2)4の倍数は12個 一の位が2or6→十の位が奇数＝各5通り 一の位が4or8→十の位が偶数＝各2通り 5*2+2=12で条件をみたす ⇒取り除いたのは4or8 (3)7の倍数は8個 作れる7の倍数11個(14,21,28,35,42,49,56,63,84,91,98)のうち 4を含むものが4個、8を含むものが3個なので 取り除いた数字は8

Name名無し20/07/19(日)16:33:18No.114328+
4月30日頃消えます[全て読む]
1列に並んだ5つの穴のどれかにウサギが1匹隠れています。
あなたは毎朝、どれか1つだけ穴を覗いてウサギがいるか確認できます。
ウサギは毎晩、1つ隣の穴に移動します。
ウサギを確実に見つけるには何日かかるでしょうか。

…No.114349+書き込みをした人によって削除されました

…No.114350そうだねx1ご丁寧にgifまであってとても分かりやすい

…No.114361+いま疲れていて精読する気が起きないが 面白い問題＆解答だね

…No.114363+捉えられることはわかったけど そのアルゴリズムが最短日数であることは言わなくていいの？ というよりも証明できるのか？

…No.114365+端を除く穴を移動しない 確率1/4✖日数？

…No.114367+書き込みをした人によって削除されました

…No.114368+穴の数に対する一般化の証明としては 多分穴n個の問題を穴n-1個の問題＋追加手順、に帰着できる系の操作で良いと思うが知らん やったら多分No.114344の手順で良いという結論になると思う そしたら日数の手ごろな上界が得られたわけなので 具体的なnについては虱潰しでより短い日数が可能か否かの判定は可能

…No.114372+>確実に見つけるには うさぎが右方向左方向決まって無い限り無いよな 確認を移動する程に確率は下がらね？

…No.114520+パリティの問題だったか

…No.114573+友達五人呼んで１日

複素関数のテーラー展開Nameあすなろ20/10/29(木)07:52:19No.114559+
21年8月頃消えます[全て読む]
　関数論を再勉強中です。細かなことはほとんど忘れています（笑）。

　1/z(z-2) と 1/z(z+2)を z = 1 でテーラー展開せよ。また、それはどのような範囲で成立するか？

　参考書の似たような問題を見よう見まねで解きましたが、間違いないでしょうか。

…No.114561+とりあえず、WolframAlpha で計算させると全く違うグラフが出力されるんだけど…

…No.114563+少なくとも俺は同じ手順で同じ答えが出たし Wolfram Alphaでも同じ結果が得られた

…No.114564+じゃ、その出力画像でも出して！

…No.114571+ >No.114564

Name名無し20/10/21(水)00:59:29No.114537+
21年8月頃消えます[全て読む]
整数解を求めよ

…No.114538+だが断る！

…No.114539+書き込みをした人によって削除されました

…No.114540+25,-6 2,1 なし

…No.114541そうだねx1(1)(x+y)(x+4y)=19 (x+y,x+4y)=±(1,19),±(19,1) (x.y)=±(-5,6),±(25,-6) (2)(x+2y)^2+y^2=17 (x+2y,y)=(±1,±4),(±4,±1) (x,y)=±(7.-4),±(9.-4),±(2.1),±(6.-1) (3)左辺≡x^2+y^2≡19≡3(mod 4) nが整数ならn^2≡0or1(mod 4)なので上記を満たす整数x,yは存在しない

…No.114542+今見返したら,が.になってるとこあるけどまあいいや

…No.114549+https://www.youtube.com/watch?v=us-NAOQLYyA これの転載か

…No.114550+１番めと２番めの考えは分かる。 因数分解と x^2+y^2 の形にして場合分けってのは理屈にあっている。 でも３番めの mod4 を考える発想ってのはどこから来るのかｗ

…No.114551+こういうのって ディオファントス方程式？ になるの？

…No.114552+平方数（２乗の数）はmod3,mod4では0か1 にしかならないから