クエスチョンName名無し20/12/27(日)19:46:12No.114717+
21年10月頃消えます 本文無し

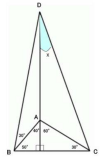
…No.114718そうだねx2tanに関する恒等式 tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) に10°を入れて計算すると tan(3×10°)=tan10°×tan(60°-10°)×tan(60°+10°) tan30°=tan10°×tan50°×tan70° 1/tan70°=tan10°×tan50°×(1/tan30°) tan20°=tan10°×tan50°×tan60° また図より tan(x)=tan10°×tan50°×tan60° となるので x=20° 幾何的な解法は他に委ねる

…No.114719そうだねx2 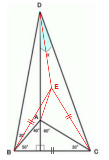（細かい角度計算は省略） △BCEが正三角形となるような点Eをとる。CAは△ABCの対称軸なので∠BEA＝∠EBA＝10°∠BDA＝10°＝∠BEAなので四角形BAEDは円に内接する。したがって∠BDE＝180°−∠BAE＝20°∠DBE＝20°＝∠BDEよりEB＝EDよって△ECDはEC＝EDの二等辺三角形となるので他の角から∠EDC＝10°と計算できる。以上より、x＝∠ADE＋∠EDC＝20°

…No.114722+ 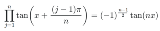>tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) これ一般化するとこうなるらしい

…No.114723+>CAは△ABCの対称軸なので∠BEA＝∠EBA＝10° 訂正：△ABC→△EBC