数学1＠2022年09月ふたば保管庫

Name名無し22/08/03(水)20:57:18No.117188+
23年4月頃消えます[全て読む]
問題：最大の自然数は偶数か奇数か？

さて？

…No.117190そうだねx3最大の自然数Nが存在したとする。
するとN+1はペアノ公理系より自然数であるが、 N<N+1 よりNが最大の自然数であるということに矛盾する。従って自然数Nは存在しない。

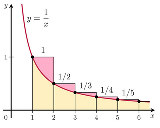
…No.117191+奇数を1、偶数を-1として自然数を強引に数えると
1-1+1-1+1-1+...
となって、この発散級数はアーベル総和法で1/2の値に対応するので
自然数は奇数の方が多い

…No.117192+巨大基数

…No.117193+円周率の最後の数字は偶数か奇数か

…No.117195+円周率はある桁以降は偶数(or奇数)しか出現しない
という可能性も考えられる
おそらく偽だと思われるが証明は難しそう

…No.117204+最大の自然数Mが素数pを因数にもたないとしたら
M*pというより大きい自然数を考えることができて矛盾、

…No.117215+>最大の自然数Nが存在したとする。
>するとN+1はペアノ公理系より自然数であるが

と簡単におっしゃるが、
Nは最大の自然数と仮定してるので
+1することは出来ないと思われる

…No.117216+できるじゃん
いを足すだけだろ？

…No.117217そうだねx1>Nは最大の自然数と仮定してるので
>+1することは出来ないと思われる

ペアノ公理系と反するじゃないかｗ
つまり、最大の自然数を仮定するとペアノ公理系と矛盾するって話。

…No.117239そうだねx1最大の自然数Nが存在したとする。
その考えられる性質とは？

Nに何を足してもNだろうし
故に何をかけてもNだし、
何で割ってもNだろう

そんなもの「自然数」に非ず

Name名無し22/07/14(木)19:15:31No.117138+
23年3月頃消えます[全て読む]
なんか始まったみたいですけど、どんなですか

…No.117141そうだねx2放送前に教えて欲しかった…

…No.117148+再放送　7/18 14:24～
https://www.nhk.jp/p/ts/Y5R676NK92/schedule/te/8PMJPN86Z8/?area=130

…No.117169+誰も見てない・・・

…No.117175そうだねx13回目でわかった　数学の番組じゃなくて
数学の難問を紹介する番組
（万人向けとは言ってない）

…No.117196+

本文無し

…No.117201+テレビつけたらたまたま四色問題やってた
ケンペの証明の誤りは
11年後証明に誤りが見つかった、
とさらっと流された

…No.117205+書き込みをした人によって削除されました

…No.117206+四色問題みたいになぜそうなっているのかに応えてくれない証明は一体……
結論は決まっているのにそれを説明する上位の論理が見当たらない
というのは数学的にあり得る話なのけ
そういう定理も存在し得ると受け入れるほかない、というのは今の時点で確定？

…No.117208+>四色問題みたいになぜそうなっているのかに応えてくれない証明は一体……
>結論は決まっているのにそれを説明する上位の論理が見当たらない
>というのは数学的にあり得る話なのけ
>そういう定理も存在し得ると受け入れるほかない、というのは今の時点で確定？
確定はしとらんだろ
まだまだ数学は奥深いからとんでもない一般理論や繋がりが根底にないとも限らない

…No.117233そうだねx1>四色問題
「６辺国や７辺国はこの中に含まれます」
説明無し？

Name名無し22/07/23(土)05:08:25No.117162+
23年4月頃消えます[全て読む]
大学数学を舐めプできるぐらいの予習はしておけ

…No.117167+大学の教養過程(学部レベル)の数学を高校時代で済ませていないと、数理分野では大成しないな

…No.117168+せめて算数チャチャチャくらいは暗算できるくらいじゃないとね
るーと２ぷらすいちぶんの　ちゃちゃ　いちたするーとのに　ちゃちゃちゃ♪

…No.117186そうだねx1高校数学も数3もほんの浅瀬でしかない

…No.117209+浅すぎる児童用プールは大人が泳ぐには浅はかすぎる

…No.117210+小学６年の算数くらいになると、解き方覚えてないと解けないようなのがある

ものすごい質問を見つけました。Name西船橋ときめきおんな学園園長22/08/08(月)06:34:29No.117207+
23年4月頃消えます[全て読む]
https://www2.rocketbbs.com/11/bbs.cgi?id=yosshy&mode=res&resto=83077

感動しました！

Name名無し22/08/05(金)19:34:30No.117194+ 23年4月頃消えます[全て読む]
来週の水曜日２３時からNHKGでポアンカレ予想やるよ

Name名無し22/01/13(木)08:16:42No.116464+
9月28日頃消えます[全て読む]
アリティ（n変数関数やn項関係のnにあたる個数）って
どうやって構成するのかよく分からないけどどうやるんだろう
ZFC公理系で自然数や順序数を作る前に
各種公理に∧だの∨だの＝だの出て来るし
これらは2項関係なのでアリティは2だけど
自然数や順序数より前の時点で出てくるアリティは
自然数でも順序数でもないと考えるしかない
じゃあアリティの正体って何なんだろう
構成するためにさらなる道具立てが必要なのか
それとももうこれ以上遡れない原始概念なのか
教えて！　数学板！

…No.116533+キューネンは読むよ
邪魔したね
じゃ

…No.116537+書き込みをした人によって削除されました

…No.116538+アリティーというのかどうか知らんが
「～が2個以上存在する」という命題を証明する場合の2というの数の基礎付けは
どこからやって来るんじゃ……
そいつは証明以前に現れる数なわけだけんども、

それとも思いつく限りの命題（を形式的に表した文）を含む集合が
形式っ的に構成できるから無問題？？
としている？？？

…No.116539+もしそうなのだとしたら
集合論で作った数とペアノ的自然数が区別できないという主張は
かなりいかがわしい
後者はこの手のアリティー（？）の処置の仕方を知らん

…No.116936+書き込みをした人によって削除されました

…No.116937+数学なんてわかりません。

…No.117094+書き込みをした人によって削除されました

…No.117095そうだねx1帰ってきたぞおおぉぉぉ
そもそも論理学にもいくつかあるということが分かった
初歩的な論理学では初歩的な変数などを並べると論理式になり
この初歩的な論理式から順序数としての自然数全体の集合ω omega が作れる
これで順序数の連番と対応するラベルとしての記号を作り
そうして素朴な論理学と同じ機能を持つフォーマルな論理学その1としての記号論理学を作れる
その後記号論理学の論理式で基数としての自然数（個数=有限基数）や自然数全体の集合（aleph0）を作って
フォーマルな論理学その2としての「無限個の変数を扱える」モデル理論を作って
n変数関数やn項関係も作ってこれで既存の数学を扱い切る
そもそもn変数関数やn項関係をモデル理論以前の論理式の仮の記法として考える場合は
それらは実は論理式に過ぎず自然数の出てくる余地はない
モデル理論でn変数関数やn項関係を「ちゃんと書く」場合
アリティとかの自然数に意味が出てくる
とりあえずこんなとこ（キューネン数学基礎論講義第I章）でバテた
この話題の本丸の第II章はまた後でゆっくりやったらあああァァァ

…No.117096+>「～が2個以上存在する」という命題を証明する場合の2というの数の基礎付けは
>どこからやって来るんじゃ……
基数としての自然数（個数・有限基数）を使うモデル理論の論理式は
基数としての自然数の定義や記号論理学の論理式の構成が要る
だからこれは実はかなり複雑な数学的対象になる
>もしそうなのだとしたら
>集合論で作った数とペアノ的自然数が区別できないという主張は
>かなりいかがわしい
有限順序数としてのペアノ的自然数を構成するには
素朴な論理式は使うが実は「アリティのあるn変数関係やn項関数」は追放しきれる
自然数も自然数全体の集合も順序数（順番）と基数（個数）の話が出てくるが
実は個数は順序数を使っておりしかも順序数よりはるかに複雑な手間が要る
順序数は比較的単純に作れる（とはいえそれなりに大変）
そういうことのようです

…No.117185+

本文無し

数学の意味Name名無し22/01/14(金)07:14:18No.116473そうだねx1 9月29日頃消えます[全て読む]
ttps://ncode.syosetu.com/n1341hk/

…No.116579+壺から来たら何なのだろうか。まだ意味がわかってないと見える

…No.116586+ネットが世間一般に普及してh抜きの必要が無くなって10年以上もたつと思うが
よほど頭を使わず漫然と暮らしてるんだろうな

…No.116593そうだねx1そりゃPC使っていながら数学や科学を否定的に批判してるようなやつだもの
数が虚無だというならPC使うなよってな

…No.116594そうだねx2そういう作風のポエムって事でいいんだよね？これ
本気でこれを書いてるならちょっと怖い

…No.116596+当時はサーバーが貧弱で、人気エロサイトとかがたまにアクセス集中で落ちてた。
アクセス解析は当時からあり、解析してみると２ちゃんが原因。
h抜いてリンク踏む奴を減らす目的もあった。
という妄想

…No.116637そうだねx1バタフライ効果って凄いよね
お互いにやり取りしている様に見えて、実際にはしてないんだぜ？
だって同じ世界に存在してないんだもん…目玉沢山詰まった人間モドキ
じゃあどこにいるのかって…人間じゃなくて人に背乗りるんだよ…目玉の意識と記録だけでな

ここの書き込み全部そうだぞｗｗｗ

…No.116638+今日は今までのどんな時より素晴らしい

…No.116645そうだねx3>バタフライ効果って
オッサンそれバタフライ効果とちゃうで

…No.117176+https://ncode.syosetu.com/n1341hk/
これかｗ

…No.117184+>ttps://ncode.syosetu.com/n1341hk/
いまだにURLのh抜いてる奴って頭がどうかしてると思う
職場でも一人でおかしなことしてそう

Name名無し22/06/29(水)10:55:21No.117103そうだねx2
23年3月頃消えます[全て読む]
本文無し

…No.117150+人間のサイズの視点から見ると15.4cmもという感覚になるが、紐を回す対象物（地球、太陽、宇宙）のサイズから見ると15.4cmなんて極微小に過ぎない
そもそも宇宙を外から紐を一周できるかどうかはまた別問題だが

…No.117158そうだねx3どこ読んでんねん

…No.117159+ベアリングボールで

…No.117160+バイクのホイールベアリング換えなきゃならない。最近金ばっかりかかる。

Name名無し22/05/25(水)02:24:25No.116969そうだねx2
23年2月頃消えます[全て読む]
解いてください

…No.116989そうだねx1１

…No.116996+>No.116982
mで両辺を割る前にmが0でないことを確認することを必要だったはず……

…No.116997そうだねx10で割るの禁止というルールは証明可能なことがらでつか
証明不可能なら公理やん

…No.117000+０で除算しました（エラー

…No.117005+証明できると言っていいかは分からんが
環を局所化する際に積閉集合に0が含まれると
環の構造が潰れて零環になってしまうから
体の構造を持つもので分母に0は置けない

…No.117012+補足すると
環の局所化と同型ではない体が存在したとしても
1=0/0=(0+0)/0=2より
1=0となりやはり自明な体となるので
体のような代数構造と零除算は両立できない

…No.117097+①数で考えるとa×b=cでa=0のときc=0すなわち0×b=0で
これは「いかなるbでも成り立つ」
これをc÷a=bに当てはめると0÷0=「いかなるbでもありうる」
②ちなみにb=0のときc=0すなわちa×0=0および0÷a=0で
これも「基本的には」「いかなるaでも成り立つ」
③でも②は0÷0=「いかなるbでもありうる」（①）というのと相容れない
④しかし0×b=0がいかなるbでも成り立つことは相変わらず正しい
⑤これら①②③④全てが正しい場合
「このように÷aが÷0すなわち0除算だったときに限り例外的にbの値は定まらなくなる性質があり
これは0÷a=bのときb=0になる通常の性質よりも優先される」
ということに結局なる
⑥c÷a=bでa=0かつc=0のときも「÷aの性質が例外的に優先される」ので
0÷0=「いかなるbでもありうる」の妥当性は通常と例外の場合を考慮してもなお保証されている
証明の方針としてはこんなもん…？

…No.117136+０以外の数÷０＝答えなし
０÷０＝すべての数

…No.117137+

0÷0=0÷0

…No.117149+https://www.youtube.com/watch?v=qrVXm5gv4tM