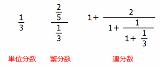数学4＠2020年07月ふたば保管庫 [戻る]

44023 B
Name名無し20/02/25(火)08:47:23No.113485+
10月28日頃消えます[全て読む]
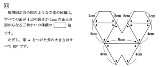
星野リゾートの若者向けホテル「BEB5」に来てますが、ハプニングプランを選んだせいで計算解かされるわ、
ルームキーがムササビだったりクソデカかったり既に最高
https://twitter.com/KmGraph/status/1231829732229971969/photo/1
…1Name名無し 20/02/25(火)08:47:33No.113486+
161184 B
本文無し

…2Name名無し 20/02/25(火)08:48:01No.113487+暗算で解くのは厳しそうかな
…3Name名無し 20/02/25(火)18:22:06No.113489+各項が短いから左から順番に足し引きすればまだ行ける部類
…4Name名無し 20/03/08(日)20:10:41No.113555+星野源

38453 B
Name名無し20/02/27(木)18:42:41No.113496+
10月31日頃消えます[全て読む]
お前らこういうの好きだろ
…20Name名無し 20/03/02(月)21:45:37No.113519+こういう抽象的な問いは
思想が入ってくるから好ましくない
出題者の思想に合致しないと不正解にされるし
健全じゃないな
…21Name名無し 20/03/02(月)22:02:29No.113520+だから、授業で「命を繋ぐため」ってのを扱って、それをまとめてからの問題なんだってばｗ
…22Name名無し 20/03/04(水)08:39:14No.113524+何言ってんの？
表現力の問題だぞ
ちゃんと書いてあるだろ
…23Name名無し 20/03/04(水)16:29:59No.113525+テストでどう書けば良いかは小学校では事前に口頭などで説明する。そうじゃないと…

(1) １＋１＝１＋１　(2) ３＋４＝３＋４
(3) ４＋７＝４＋７　(4) ６−５＝６−５

なんて珍回答した答案に○をやらんといけなくなる。
…24Name名無し 20/03/05(木)11:36:02No.113535+あああ
表現力のテストなのか
こりゃ難しいわ。
…25Name名無し 20/03/05(木)11:44:55No.113536+
4500 B
>何言ってんの？
>表現力の問題だぞこれで○くれないならおれはグレる。
…26Name名無し 20/03/05(木)21:58:21No.113537+えーｗ　じゃ

「１＋２＝１＋２」という回答に何で○くれないの？
○くれなきゃぐれるぞ！

ってのをどうやって対処するんだよｗ
安易に○やって、俺も私もって皆に広がったら収拾つかん
…27Name名無し 20/03/07(土)02:27:02No.113539+〇×付ける時点でゆとりがない
…28Name名無し 20/03/08(日)10:52:28No.113545+「卵を美味しく食べてくれる捕食者のため」
…29Name名無し 20/03/08(日)20:09:37No.113554+ガールズパンツァー

82653 B
Name名無し20/02/18(火)03:25:46No.113476+
10月21日頃消えます[全て読む]
灘中学の算数
…1Name名無し 20/02/18(火)10:43:30No.113477+大きい正四面体の体積二つから小さい正四面体の体積一つを引けば良いから
2*(4^3 * V) - (2^3 * V)=(128-8)*V=120*V
120倍
…2Name名無し 20/02/20(木)23:06:16No.113478+1辺が2cmの三角すいが何個入るか数えたら良いのでは
…3Name名無し 20/02/22(土)23:51:16No.113479+書き込みをした人によって削除されました
…4Name名無し 20/02/22(土)23:52:41No.113480+1辺が1cmの三角すいを何個使うと1辺が4cmの三角すいになるの？

1辺が1cmの三角すいを何個使うと1辺が2cmで高さ2㎝の三角柱になるの？
…5Name名無し 20/02/27(木)14:43:29No.113494+書き込みをした人によって削除されました
…6Name名無し 20/02/27(木)18:01:23No.113495+>1辺が1cmの三角すいを何個使うと1辺が4cmの三角すいになるの？
25個かな
…7Name名無し 20/03/01(日)23:19:40No.113517+未精査のまま提出。
…8Name名無し 20/03/02(月)08:25:27No.113518+そんな足し算しなくても体積比で簡単に出るでしょ
4^3=64個だよ
…9Name名無し 20/03/08(日)20:02:10No.113551+数学オリンピック
Name名無し20/01/29(水)06:53:35No.113404+ 10月01日頃消えます[全て読む]
積分がわからない人でも体積を求められるいい公式を教えましょう。

H:高さ
T:上面積(高さHでの断面積)
Y:中面積(高さH/2での断面積)
U:底面積(高さ0での断面積)

とすると

体積V = H(T+6Y+U)/4
…1Name名無し 20/01/31(金)07:35:51No.113414+今は咳分が流行ですね
…2Name名無し 20/01/31(金)09:06:33No.113415+↑
C国はどれだけの人数が感染してるかの咳分定数を隠すし、不定咳分だな。
…3Name名無し 20/02/04(火)02:59:20No.113419+>体積V = H(T+6Y+U)/4
↑この公式で断面積一定の立体だとすると
T=Y=U だから

V =H(T+6Y+U)/4 =2HT

になって、明らかに間違ってるけど？
…4Name名無し 20/02/04(火)03:02:31No.113420+そういう近似公式をつくりたいなら
断面積を被積分関数にしたガウス求積でも使った方がいいんじゃね？
…5Name名無し 20/02/05(水)19:18:57No.113422+>>３
間違えてた

H:高さ
T:上面積(高さHでの断面積)
Y:中面積(高さH/2での断面積)
U:底面積(高さ0での断面積)

とすると

体積V = H(T+4Y+U)/6
だったわ
…6Name名無し 20/03/03(火)12:22:34No.113521そうだねx1
6048 B
白と黒の体積が同じなの？冗談よせやい

…7Name名無し 20/03/03(火)19:51:28No.113522+錐体、あるいはそれを底面に平行に切断した立体だと成り立つけどそれより複雑な形になるほどずれてくる
…8Name名無し 20/03/03(火)22:11:13No.113523+
51873 B
遠い銀河までの距離の計算と同じ感じがする

…9Name名無し 20/03/08(日)20:00:18No.113550+分かった積もり

109169 B
Name名無し20/01/30(木)21:12:22No.113413そうだねx1
10月03日頃消えます[全て読む]
本文無し
…3Name名無し 20/02/06(木)23:45:26No.113425+97.5
14|1365
126
105
98
70
70
0
?
…4Name名無し 20/02/08(土)23:44:07No.113427+
145921 B
本文無し

…5Name名無し 20/02/09(日)02:05:10No.113428+やったぜ。あってたわ
…6Name名無し 20/02/11(火)23:08:21No.113435そうだねx1その勢いでスレ問題も証明して
…7Name名無し 20/02/12(水)16:13:40No.113436+ガム,クッキー,チョコレートの値段をそれぞれx,y,z円とおくと与えられた条件から立式すれば

x=75
x=y-40
z=?

を解けばいい。ｚについて情報がないので行列に直すと

１　０　０　｜　x　　　75
１　-1　０　｜　y　＝　-40
０　０　０　｜　z　　　０

zについて情報がないので拡大係数行列のランクは2だから自由度は1。
∴z=cとなる。ただしcは任意定数。
つまり定数であれば何円でも正解。
…8Name名無し 20/02/13(木)15:50:10No.113444+一応小学生の問題なんで
…9Name名無し 20/02/14(金)06:56:09No.113446+
15444 B
ガムは75円、クッキーより40円安い、チョコレートはいくら？

…10Name名無し 20/02/15(土)19:13:54No.113456+>つまり定数であれば何円でも正解。
それでは (-e+iπ) 円でも正解の要素になるのでは？
貨幣による価値尺度は測度の概念だからせめて非負整数だろうに
…11Name名無し 20/02/15(土)20:00:22No.113457+マイナス金利！
…12Name名無し 20/02/15(土)20:46:36No.113458+>マイナス金利！
金利は割合なので円やドルといった単位は無く無次元！

96772 B
神戸の有名私立中学校入試問題Name名無し20/02/10(月)01:31:05No.113429+
10月13日頃消えます[全て読む]
つい先ほど行われたナ〇中の入試問題です。
全く歯が立ちませんでした。答えは分かっています。
解き方をどなたかお教え願いませんか。
宜しくお願い致します。
…1Name名無し 20/02/10(月)01:33:06No.113430+
461698 B
問題文が見えにくいので少し大きくしました。

…2Name名無し 20/02/10(月)10:30:39No.113431+ナン中出身だけど、月曜で386個？

>答えは分かっています。
秘密かよ
…3Name名無し 20/02/10(月)13:35:29No.113432+説明を簡略化するためにここでは祝日を考慮せずに　月〜金曜日を平日　土曜日と日曜日を休日とする
6月と9月について　月に5日ある曜日は2つあり　そのうちの片方は共通する
加えて6月と9月は一ヵ月の日数が同じため　月生産数の差 372-366= 6個 は共通しないもう片方の曜日の生産数の差　したがって平日の生産数は休日の生産数より6個多い
どの月も休日の数は8,9,10日のいずれかであり　仮にそれらの生産数を平日の生産数と同じにすると　月生産数はそれぞれ48個,54個,60個増える
これによって6月,9月の生産数は月の日数(30)の倍数になる必要があるので　休日の数は6月で8日, 9月で9日ある　
また　この仮定によって月生産数は420個になるので　平日の生産数は420÷30= 14個, 休日の生産数は14-6= 8個
月に5日ある曜日は6月と9月で前に1つずつずれるので　週に5日ある曜日は6月で木金, 9月で金土 となる　したがって6/1は木曜日
また 7月の月生産数は平日が21日, 休日が10日あるので14*21+8*10= 374個
…4Name名無し 20/02/10(月)19:33:04No.113433+youtubeに上がってんじゃん

64862 B
Name名無し20/02/06(木)22:37:06No.113424+
10月10日頃消えます[全て読む]
本文無し
…1Name名無し 20/02/08(土)08:14:37No.113426+ﾋｴｯ…ひ、人生時計…！

9562 B
Name名無し20/01/01(水)13:38:41No.113366+
9月04日頃消えます[全て読む]
適切な演算子を用いて数式を満たせ
…1Name名無し 20/01/01(水)16:54:01No.113367+1*(2+3)*4*5*(6+7)+8*9*10=2020
…2Name名無し 20/01/03(金)08:39:37No.113368そうだねx210項演算子*を*(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10)=2020で定義すると
*(1,2,3,4,5,6,7,8,9,10)=2020
…3Name名無し 20/01/03(金)11:30:04No.113369+1+2+[√（3＊456789）]-10
…4Name名無し 20/01/04(土)08:05:13No.113372+1+2+[√（3＊456789）]-10 =
1,163.626755204237
…5Name名無し 20/01/04(土)15:48:18No.113373そうだねx1>1+2+[√（3＊456789）]-10 =
>1,163.626755204237
済まない
1+2+[3＊√(456789）]-10
だった
[ ]はガウス記号
…6Name名無し 20/01/07(火)20:33:35No.113374+ガウス記号は演算子・・・？
…7Name名無し 20/02/04(火)20:44:08No.113421+ガウス記号は単項演算子だよ．

1904724 B
Name名無し20/01/29(水)14:54:44No.113405+
10月02日頃消えます[全て読む]
最近数学を勉強しようと思っているのですが恐らく算数の段階のこの問題にぶち当たって誰にも聞ける人もいず困ってます
どうかどうしてこの２つの計算の答えが違うのか教えて下さるとありがたいです
…1Name名無し 20/01/29(水)17:44:26No.113406+算数の＋,−,×,÷にはルールがあって
特に　a÷b÷c　のような割り算だけの場合を計算するときは
(a÷b)÷c　のように左から計算するルールでした。
なぜこのルールがあるかというと
8÷4÷2 = (8÷4)÷2 = 1
8÷4÷2 = 8÷(4÷2) = 4
と違う答えになるからです。このことを数学の専門用語で除法について結合法則を満たさないと言います。
また分数は a/b = a÷b のことですから
a/b/c = (a/b)/c と計算しないといけません。
…2Name名無し 20/01/29(水)17:44:43No.113407+なのでおかしな点は二番の12/25×25をけるところが間違いです。なぜなら先に1÷12をしないといけないのに12÷25について考えています。なので正しくは
((1÷12)×25) / (25×25) = (0.08333...×25)/625 = 0.003333...
となります。

数学的にはこのような複数の意味で捉えることができる式を立てることは正しくありません。
どうしてもこのように書きたい場合には間違いが起きないように括弧を付けたり、その略記として分数の線の長さを強弱をつけてどこまでが分母であるかをきちんと明記する必要があります。
なので8÷2(2×2)などの式は数学的には正しくないです。
式を立てるときは計算する人に誤解を与えないようにしましょう。
…3Name名無し 20/01/29(水)19:17:55No.113408そうだねx1
1791184 B
なるほど！
ようするにこの画像のに2のように、分母にカッコをつければいいわけですね！ありがとうございました！
…4Name名無し 20/01/29(水)21:29:59No.113409+
2377 B
分数の中に分数がある繁分数では、分数の横線（括線と呼ぶ）の長さで分子と分母の関係を明確にする必要がある
スレ画の場合だと①は下の括線を長く、②は上の括線を長く書く
…5Name名無し 20/01/29(水)22:00:44No.113410+ホントは割り算や分数と同じように、累乗も順番を明記しなきゃダメダメなんだよな。

2^3^2 を (2^3)^2 と解釈すると 36 だ。
ところが 2^(3^2) と解釈すると 512 だな。

でも、普通は下のように解釈する。
正規分布の式でも　e^-x^2/2 となるが右側から計算するお約束
…6Name名無し 20/01/29(水)22:16:05No.113411+>1580300999877.gif
謎が解けました
ありがとう
…7Name名無し 20/01/30(木)14:45:07No.113412+はぇーすっごい頑張れ！！

4269 B
Name名無し20/01/16(木)00:25:53No.113378そうだねx1
9月18日頃消えます[全て読む]
正五角形ABCDEに占める
三角形ACDの面積の比率は５０％以下らしい
この比率を表す数式を求めよう
…1Name名無し 20/01/16(木)05:21:41No.113379+φ=(1+√5)/2とすると
BC//AD, ED//AC, BC:AD=ED//EC=1:φより
三角形ABC:三角形ACD:三角形ADE=1:φ:1
三角形ACD/五角形ABCDE=φ/(φ+2)=1/√5
…2Name名無し 20/01/17(金)01:43:32No.113380+>BC:AD=ED//EC=1:φより
BC:AD=ED:AC=1:φのミス
…3Name名無し 20/01/17(金)02:41:21No.113382+イイ問題やねー面白かった
ＢからＡＣに平行線を引きＣＤの延長線との交点をＧとする
またＡＢの延長とＣＤの交点をＦとする。△ＡＣＤ∽△ＢＧＣ、ＡＤ＝ＡＣ＝aとし正五角形の一辺を１とすると、
ＡＤ：ＢＣ＝ＣＤ：ＧＣなのでＧＣ＝1/aとなる。
ＦＢ：ＢＡ＝ＦＧ：ＧＣなので
(aー1/a)：１／a＝a：１となり2次方程式が出来てaの解は
(1+√5)/2となる。
△ＡＧＣ＝△ＡＢＣなので、面積比は底辺の比になる。
(√５ー１)：２：(√５ー１)となる
この計算結果から５０％以上では無く
０．４４７２…約４５％です
…4Name名無し 20/01/17(金)02:42:36No.113383+↑御免５０％以下と書いていましたね
謝ります。
…5Name名無し 20/01/18(土)15:05:35No.113384+謝・蓮舫
[0] [1] [2] [3] [4] [5]