Name名無し20/01/16(木)00:25:53No.113378そうだねx1
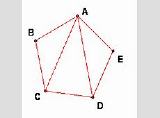
9月18日頃消えます 正五角形ABCDEに占める
三角形ACDの面積の比率は５０％以下らしい
この比率を表す数式を求めよう

…	1Name名無し 20/01/16(木)05:21:41No.113379+φ=(1+√5)/2とすると BC//AD, ED//AC, BC:AD=ED//EC=1:φより 三角形ABC:三角形ACD:三角形ADE=1:φ:1 三角形ACD/五角形ABCDE=φ/(φ+2)=1/√5

…	2Name名無し 20/01/17(金)01:43:32No.113380+>BC:AD=ED//EC=1:φより BC:AD=ED:AC=1:φのミス

…	3Name名無し 20/01/17(金)02:41:21No.113382+イイ問題やねー面白かった ＢからＡＣに平行線を引きＣＤの延長線との交点をＧとする またＡＢの延長とＣＤの交点をＦとする。△ＡＣＤ∽△ＢＧＣ、ＡＤ＝ＡＣ＝aとし正五角形の一辺を１とすると、 ＡＤ：ＢＣ＝ＣＤ：ＧＣなのでＧＣ＝1/aとなる。 ＦＢ：ＢＡ＝ＦＧ：ＧＣなので (aー1/a)：１／a＝a：１となり2次方程式が出来てaの解は (1+√5)/2となる。 △ＡＧＣ＝△ＡＢＣなので、面積比は底辺の比になる。 (√５ー１)：２：(√５ー１)となる この計算結果から５０％以上では無く ０．４４７２…約４５％です

…	4Name名無し 20/01/17(金)02:42:36No.113383+↑御免５０％以下と書いていましたね 謝ります。

…	5Name名無し 20/01/18(土)15:05:35No.113384+謝・蓮舫