数学2＠2020年03月ふたば保管庫 [戻る]
画像ファイル名：1577199163247.png-(10264 B)10264 B
Name名無し19/12/24(火)23:52:43No.113340+
20年8月頃消えます[全て読む]
メリー
ぼっちmath！
…1Name名無し 19/12/25(水)00:09:33No.113341+パンツ！
画像ファイル名：1576493343425.png-(460533 B)460533 B
Name名無し19/12/16(月)19:49:03No.113323+
20年8月頃消えます[全て読む]
ニホニウムの次ってまだなの？
…1Name名無し 19/12/16(月)21:06:27No.113324そうだねx1ニホニウムは113番だけど今は118番まであるよ
…2Name名無し 19/12/17(火)21:30:25No.113327+119番は作れそうなのか？
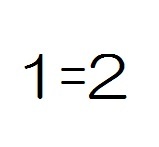
画像ファイル名：1565655414700.jpg-(3545 B)3545 B
Name名無し19/08/13(火)09:16:54No.112690そうだねx1
3月30日頃消えます[全て読む]
1=2 の証明スレ
数学好きなら2つや3つくらい目にしてるはず
とりあえず１つめ
1=1+0+0+0+0+…
=1+(1-1)+(1-1)+(1-1)+(1-1)+…
=1+1-1+1-1+1-1+1-1+…
=1+1+(-1+1)+(-1+1)+(-1+1)+(-1+1)+…
=1+1+0+0+0+0+…
=2
…42Name名無し 19/09/04(水)20:53:26No.112857+まだやってるのかｗ
…43Name名無し 19/09/06(金)22:36:40No.112861+直線 y = 2xを考える。
関数は従属変数と独立変数が1対1対応しているので、x座標の数とy座標の数は等しい。…①

また、このグラフでは定義域[0,1]において値域は[0,2]である。…②

①②より、幅が1の区間と幅が2の区間に存在する点の数は等しい。
よって、1 = 2
…44Name名無し 19/09/07(土)06:20:28No.112862+A + 1

ってのは
すべての整数の中で最大のものを A
としてるので、おかしい
存在しない
…45Name名無し 19/09/13(金)05:25:17No.112887そうだねx1１＝２
２＝１
３＝２
４＝２
５＝１
６＝２
７＝２
８＝２
９＝2.5
１０＝2.5
１１＝4.5
では１２＝いくつ？
と言うクイズを出されてイライラしたのを思い出した
なんでもかんでも＝でつなげればいいってモンじゃないってことをキモにメイジテオイテクダサイ
…46Name名無し 19/09/14(土)12:01:56No.112898そうだねx13.5
…47Name名無し 19/09/14(土)17:07:07No.112899そうだねx1おれは
4＝1
なんだけど
…48Name名無し 19/09/14(土)17:43:34No.112900そうだねx1>おれは
>4＝1
>なんだけど
9＝1、10＝2でも良い
…49Name名無し 19/12/04(水)20:13:59No.113277そうだねx1 448877 B
>No.112695
これを思い出した
…50Name名無し 19/12/14(土)23:02:30No.113321+>No.112695
これは興味深いな。
つまり斜辺の「傾き成分」とでも呼ぶべきものが１㎝分だということになるのではないか？
…51Name名無し 19/12/16(月)01:31:14No.113322+L^2ノルムとかマンハッタン距離でググれ
画像ファイル名：1575892755063.jpg-(69340 B)69340 B
Name名無し19/12/09(月)20:59:15No.113307+
20年7月頃消えます[全て読む]
マヨナラってどこに消えたの？
ニコラスケイジにでも異世界転生してるの？
…1Name名無し 19/12/09(月)21:17:30No.113308+この世界からマヨナラ〜
…2Name名無し 19/12/12(木)15:54:06No.113315+マヨナラじゃなくてマヨラナでは
画像ファイル名：1572217449772.png-(63533 B)63533 B
Name名無し19/10/28(月)08:04:09No.113161+
6月14日頃消えます[全て読む]
質問なのですが3個のものから0個のものを取り出す
具体的取り出し方って何になりますのん？
…2Name名無し 19/10/28(月)16:42:33No.113164+0個取り出す=取り出さない=1通り
…3Name名無し 19/10/28(月)23:17:27No.113167+( 1, 2, 3 )からr個を取り出す取り出し方を列挙するプログラムがあったとすると、
r=1のときの出力は( (1), (2), (3) )という3要素のリスト、
r=2のときの出力は( (1, 2), (1, 3), (2, 3) )という3要素のリスト
r=3のときの出力は( (1, 2, 3) )という1要素のリスト
や

>No.113162
>それぞれ0個取り出す
r=0のときプログラムは何を出力すべきやと思ーう？

>No.113164
>0個取り出す=取り出さない=1通り
r=0のときプログラムは何を出力すべきやと思ーう？
…4Name名無し 19/10/29(火)00:10:30No.113168+未定義を出力する
不完全なプログラム
…5Name名無し 19/10/29(火)01:30:21No.113169+> r=0のときプログラムは何を出力すべきやと思ーう？
( () ) という1要素のリスト
…6Name名無し 19/10/29(火)01:49:39No.113170+空集合という要素の無いの集合体が選ばれただけ
…7Name名無し 19/10/29(火)01:51:25No.113171+書き込みをした人によって削除されました
…8Name名無し 19/10/29(火)01:52:11No.113172+>No.113169
$cmb = Combination->new(1, 0);
$cmb->reset();
while ($cmb->move_next()) {
　　print "( ", $cmb->current(), " )\n";　// 未定儀が出力
}
で未定儀が出力されてしまうま…
…9Name名無し 19/10/29(火)01:53:53No.113173+書き込みをした人によって削除されました
…10Name名無し 19/10/29(火)02:03:32No.113174+ｽﾏﾝ空のリストのリストを出力した場合は
No.113172では未定儀出力にはならなかったorz
ただﾏｼﾞ単純に書いたら空のリストが出てきてしまい、
No.113169になるわけでもなかった、
…11Name名無し 19/12/08(日)09:24:00No.113297+0個の物から0個の物を取り出すのは1通り
1個の物から0個の物を取り出すのは1通り
0個の物から1個の物を取り出すのは0通り

この世の不思議
画像ファイル名：1567895985696.jpg-(16603 B)16603 B
算数 → 数学Name名無し19/09/08(日)07:39:45No.112866+
4月25日頃消えます[全て読む]
算数から数学になったきっかけは！マーク
最初は69！で遊んでたけど、69！以上はどうすれば求められるか？
！の式がなして e=2.71828 に絡むの？
！がその内 sin cos や i にまで進出して来る。
とっても不思議だった。重い原子核と素数が絡むなど。

算数から数学に興味が発展したきっかけを聞かせて下さい。
…3Name名無し 19/09/11(水)00:52:53No.112880+階乗じゃなくて？
…4Name名無し 19/09/11(水)23:33:19No.112883+「フーリエの冒険」とか「平面の国の不思議な物語」とか
「ゲーデルエッシャーバッハ」とか読んで数学の世界が好きになった
…5Name名無し 19/09/13(金)20:29:17No.112896+きっかけは円周率
3.14159265358979…とずっと続くと聞いて興味を持った
…6Name名無し 19/09/14(土)21:31:50No.112901+>階乗じゃなくて？
階乗の式が e になるのが不思議だった
SIN COSは病気で1カ月ぐらい入院していて置いてきぼりに
グレゴリー・ペレルマンがトポロジーを使わずに証明してみせたのが好き
…7Name名無し 19/09/15(日)04:53:42No.112904そうだねx1自然対数って何が自然なんでし
た
っけ
？
…8Name名無し 19/09/15(日)08:02:54No.112905+69!=171122452428141311372468338881272839092270544893520369393648040923257279754140647424000000000000000
…9Name名無し 19/09/16(月)21:28:24No.112915+書き込みをした人によって削除されました
…10Name名無し 19/11/26(火)00:28:29No.113254+e^(iπ)=-1

「なんでこうなるのだろう？」と思ったね。
…11Name名無し 19/12/05(木)14:37:17No.113279+普通は代数から入るような気がする
式にxとかyとか出てくると数学っぽいなと思う
…12Name名無し 19/12/06(金)21:44:24No.113291+ 132525 B
>！マーク
ぶっちゃけ、たまには「？マーク」のことも思い出してあげて欲しいのですよ…。https://en.wikipedia.org/wiki/Minkowski's_question-mark_function
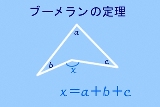
画像ファイル名：1572442003205.jpg-(99735 B)99735 B
Name名無し19/10/30(水)22:26:43No.113184+
6月17日頃消えます[全て読む]
右の定理を証明する問題みたいに
中学生の範囲で解き方考え方がたくさんある問題スレ
もちろんこの定理の証明を20個ぐらい挙げてもOKです。
…9Name名無し 19/11/03(日)20:35:31No.113222+平行四辺形＋三角形に分割
大三角形−小三角形
上下に分割して移動し、平行四辺形をつくる
…10Name名無し 19/11/05(火)04:27:36No.113224+線で囲まれた面積は、ドットに換算して面積を出す数式またはアルゴリズムってあるの？
…11Name名無し 19/11/05(火)20:34:34No.113225+> 線で囲まれた面積は、ドットに換算して面積を出す数式またはアルゴリズムってあるの？
台形公式使ったりとか、そう言うこと？
モンテカルロ法で解くのもあるけど
…12Name名無し 19/11/07(木)10:28:30No.113228+地図とか公図とかスキャナして範囲を指定すると面積が出てくるとか・・
Ｒや長さを指定すると囲まれた面積が出てくるみたいな

数式だと誤差のない面積が求められるんだけど、誤差があるけど面積を求めて、数式の正しさを証明する感じのもの？
…13Name名無し 19/11/09(土)12:32:07No.113231+モンテカルロ積分とか準積分とか
…14Name名無し 19/11/09(土)13:20:56No.113232+直線は２元１次方程式で表せるけど、囲まれた部分の内部にあるか外部にあるかの判断は結構難しいアルゴリズムになるんじゃなかったっけ？

大体往年の8-16bitのアドベンチャーゲームのpaintアルゴリズムが結構時間かけて描いていたような。
…15Name名無し 19/11/09(土)19:06:06No.113233+凸図形なら簡単
凹図形は凸図形の和とみなせば凸図形のやつで逝ける
…16Name名無し 19/11/09(土)19:12:18No.113234+書き込みをした人によって削除されました
…17Name名無し 19/11/09(土)19:13:01No.113235+Paintアルゴリズムは境界色か描画色に行き当たるまで隣接画素を描画色で塗りつぶしていく
のが基本
（描画色を停止条件に含めるのは、含めないとドーナツ状図形の塗りつぶしが終わらなくなるため

ただしすでに描画色でなんか書かれている可能性がありかつそれを無視せねばならない場合は
境界色かすでに塗りつぶした画素に行き当たるまで、という修正した条件でヤル

条件にあたる隣接画素をもれなく塗りつぶすにはスタックが要る
書いたらﾜｶﾙ
…18Name名無し 19/12/05(木)14:47:55No.113280+数列a_1, a_2, a_3, ... は任意の正の整数i, j に対して
a_(i+j) <= a_i + a_j
を満たす．このとき，
a_1 + a_2 / 2 + a_3 / 3 + ... + a_n / n >= a_n
が成り立つことを示せ．

この問題は代数でも組合せでも解ける
代数で解くのは簡単だけど組合せで解くのは難しい
他にも解き方があるかも
画像ファイル名：1574652715654.jpg-(141340 B)141340 B
Name名無し19/11/25(月)12:31:55No.113249+
20年7月頃消えます[全て読む]
-100度の空気に当たって加熱するとは　？
…1Name名無し 19/11/25(月)17:31:32No.113252そうだねx1加熱される側が-150℃ぐらいだったとか
…2Name名無し 19/12/02(月)04:48:24No.113269そうだねx2常温で使う低圧の空気入れ程度でも、断熱圧縮により
ずっと触ってられないくらいは熱くなるからなあ
…3Name名無し 19/12/02(月)15:04:43No.113270そうだねx1音速を超えると空気が横に逃げないので圧縮される
画像ファイル名：1575217491218.png-(147167 B)147167 B
Name名無し19/12/02(月)01:24:51No.113268+
20年7月頃消えます[全て読む]
本文無し
画像ファイル名：1571820791975.jpg-(40091 B)40091 B
Name名無し19/10/23(水)17:53:11No.113147+
6月10日頃消えます[全て読む]
こんなんあかんがな
と思ったが
ある瞬間、栗饅頭が倍になる時、両端の相対速度が光速を超えるタイミングがあり、その時以降、それ以上大きくならないらしくて大丈夫らしい
が、しかし
その遥か以前
このロケットが地球から遠ざかる、はるかに有限な速度を、栗饅頭が倍になる速度が超える時
やっぱり地球は無数の栗饅頭に飲み込まれ、潰れる気がする
…22Name名無し 19/10/31(木)22:50:02No.113191+>「円板（正方形）を有限個の破片に分け、それらを集めて同じ面積の正方形（円板）にすることができるか」
定規とコンパスだけでできたらネ申
…23NameNo.113158 19/10/31(木)23:53:56No.113192+ 212520 B
>定規とコンパスだけでできたらネ申
ぶっちゃけ、双曲平面（ボヤイ＝ロバチェフスキー幾何学）では可能なのですよ。
…24Name名無し 19/11/02(土)12:19:41No.113202+>>定規とコンパスだけでできたらネ申
>ぶっちゃけ、双曲平面（ボヤイ＝ロバチェフスキー幾何学）では可能なのですよ。
mjk、
双曲平面上での図形の平行移動や回転ってどうなの？
どうなっちゃうの？？
…25Name名無し 19/11/02(土)20:11:44No.113205+>双曲平面上での図形の平行移動や回転ってどうなの？
双曲平面の曲率に従うだけのこと
ただ曲率の補正演算がメンドクサイことになるけど
…26Name名無し 19/11/02(土)21:36:00No.113209+書き込みをした人によって削除されました
…27Name名無し 19/11/02(土)21:37:31No.113210+メンドクサイ曲率の補正演算の上で遂行される図形操作の中に
円積問題を解く手順が存在すると断言できるのは概略なんでや…？
なんかこう見通しのよくなる変換でもあるの？？
…28Name名無し 19/11/02(土)21:49:46No.113212+>円積問題を解く手順が存在すると断言できるのは概略なんでや…？
曲率次第で有理数体から出発して体のある元の平方根を追加して新しい体を得るという
操作の有限回の繰り返しで円周率を含むような体が得られるから（その場合曲率は超越数になる）
…29Name名無し 19/11/03(日)12:46:46No.113217+なんか
ある物体を原子のレベルまで分解したら
その材料の原子で他のものに出来る
的な話なだけの気がしてきた
そんなもん、なんぼでもできる
神の粒子、とか想定しだしたら、
一瞬のきらめき一つから、宇宙も出来る
…30Name名無し 19/11/24(日)18:53:27No.113246+書き込みをした人によって削除されました
…31Name名無し 19/11/26(火)00:02:45No.113253+>ぶっちゃけ、「できる」のですよ。

>平面においては、非可測な部分に分解することによって曲率は保存されないためである。

ざっくり言うと、微分積分な世界に持ってくわけね。
[0] [1] [2] [3] [4] [5] [6]