数学3＠2021年07月ふたば保管庫

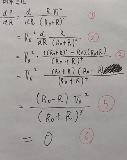
Name名無し21/03/14(日)17:08:09No.114949+
22年2月頃消えます[全て読む]
②から③の微分するやり方が分からないので
やり方を教えて下さいお願いします。

…No.114950+③の分子が問題なんだろ？
(R0+R)^2 = R0^2 + 2R0R + R^2 より

③の分子は　R'(R0+R)^2 - (R0^2+2R0R+R)'R となるから
= 1(R0+R)(R0+R) - (2R0+2R)R
= (R0+R-2R)(R0+R)
= (R0-R)(R0+R)

となるんじゃなかろうか

…No.114951+それ以前に微分出来ないんですよ。
受験経験者の常識みたいな微分の公式でも
あるんでしょうか。
分母と分子をRで割って
dp/dr＝dp/dA×dA/drみたいなことすれば出来ますか

…No.114952+

本文無し

…No.114953+>それ以前に微分出来ないんですよ。
>受験経験者の常識みたいな微分の公式でも
>あるんでしょうか。
商の微分が分からんってこと？
(f / g)' = (f' g - f g') / g^2

…No.114954+商の導関数は高校の数学IIIで習う
ここの9ページ目でも見てちょ
 http://skredu.mods.jp/a01/3%20bibun.pdf

…No.114955+見てみますありがとうございます。

…No.114956+あと合成関数の微分知らないと(R_0 + R)^2の微分は多少面倒臭い
これは↑の12ページ目に乗ってる

…No.114957+dp/dr＝dp/dA×dA/drみたいなヤツですよね
名前は忘れてたけどそれは今でも時々使います。

…No.114958+それそれ
後は積の微分公式と商の微分公式はよく使うので覚えておいた方が良

…No.114959+良い

Name名無し21/02/06(土)19:12:31No.114826+
21年12月頃消えます[全て読む]
こういう渦巻が一筆書きできるか
簡単に見分ける方法ってある？

…No.114870+書き込みをした人によって削除されました

…No.114874+書き込みをした人によって削除されました

…No.114875+書き込みをした人によって削除されました

…No.114883+>交点が奇数の場合→渦は中心で折り返している＝一筆書き可能
>交点が偶数の場合→渦は2本の閉曲線でできている＝一筆書き不可

それをどうやって知るの？ｗ

…No.114895+>それをどうやって知るの？ｗ
巻き数が多い場合ってことかな
塗る場合でも塗りきれるかはわからないよね

…No.114906+渦巻きに点対称図形という縛りがつくなら
中心が定まり、そこから放射する半直線と渦巻きの
交差点数の偶奇も定まる、
ﾖｶﾝ

…No.114917そうだねx1結局渦巻に対してどういう操作が出来るのかは渦巻がどう定式化されてるかに依るよね

…No.114920+>渦巻きに点対称図形という縛りがつくなら
三つ巴とかの奇数巴だとダメだね

…No.114921+目で見て数えられるなら数えれば済むわけで一筆なのかＮ筆なのかわからない場合は一般的な法則を作れないのでは

…No.114933+

もみぞうでﾋﾛﾀ

Name名無し21/02/11(木)13:42:15No.114841+
22年1月頃消えます[全て読む]
コンピュータの勉強をすると離散数学が問われますが、そもそも離散数学とは何なのでしょうか？
連続しない数を扱う学問と言われても、数は連続してないから算数全てが離散数学なんじゃ？と思ってしまいます。
きっと認識が足りていないので、文系が理解し易い表現が可能な優秀な数学板住人の方に説明願いたいです。

…No.114843+この離散という言葉が連続の対義語として用いられているのは確かだけどじゃあその連続って何だって話だよね
この場合の連続っていうのは「実数の連続性」という公理の事を指してる
自然数や整数、有理数はこの「実数の連続性」が成り立たないので離散と言われてる
https://syllabus.hosei.ac.jp/files/1420511.pdf

…No.114844+つまり数は連続というけどその連続という言葉が意外にも厳密に数学的に定義された言葉で日常生活で使う連続という言葉と少し乖離があるから混乱を招くんだと思う

…No.114845+ご教示ありがとうございます。
ものすごく丸めて自然数を扱うか実数を扱うかの違いと理解しました。
正解では無いでしょうが認識が進歩した気がします。

…No.114846+>ご教示ありがとうございます。
>ものすごく丸めて自然数を扱うか実数を扱うかの違いと理解しました。
>正解では無いでしょうが認識が進歩した気がします。
だいたいそんな感じ
有理数も離散なのは意外かもしれないから注意すべきポイント

…No.114847+無限や無限小、連続性を扱う解析分野
幾何学的直観が裏に控えてる幾何学

はあんまり離散的対象を直接には扱わない

…No.114848+>連続性を扱う解析分野
関数の連続性と実数の連続性はまた別物だから多分この文脈で解析学ってまとめちゃうと混乱すると思う

…No.114849+>>連続性を扱う解析分野
>関数の連続性と実数の連続性はまた別物だから多分この文脈で解析学ってまとめちゃうと混乱すると思う
別モノってほどか？
ホモトピー性とかの連続性はぐっと幾何学的になるけどさ

…No.114860+「実数の連続性」は実数特有？の公理だけど関数というか写像の連続性はどんな位相空間でも議論できるからね

…No.114871+コンピュータサイエンスに関連する範疇だと

1. 集合理論 (AかつB, AまたはB, etc..)
2. 順列、組み合わせ (全てのパターンを漏らさず効率よく調べるアルゴリズム)
3. 木、グラフ (SNSの繋がりや、地図や路線アプリの経路検索)
4. 整数理論 (公倍数、公約数や割り算の余りを利用した計算、暗号理論の基礎になる)
あたりか

微分積分、線形代数、確率統計以外の数学をそこに押し込んでる場合が多い

…No.114872+有限体の数学が離散数学
、という印象

Name名無し21/01/17(日)20:11:58No.114783+ 21年12月頃消えます[全て読む]
n^2+4とnが共に素数となる自然数nって無限にある？

…No.114784+知りません

…No.114785+それを記すには、余白があまりにも狭すぎる

…No.114805+書き込みをした人によって削除されました

…No.114806+書き込みをした人によって削除されました

…No.114862+

有名大学の過去問じゃないか

…No.114863+俺の母校じゃん

…No.114864そうだねx1検索すると…

「ブニャコフスキー予想」はウクライナの数学者ヴィクトール・ブニャコフスキーが1857年に提示した予想なのですが、未だに完全な証明が与えられていません。しかし反例も見つかっていないので、恐らく成り立つだろうと肯定的に支持されています。

この予想によれば、その表でせるような素数は無数に存在することが予想できます。･･･とはいえ、どのでが素数になるかについては全く別問題です。ハッキリ言って本問は捨て問です(笑)。

とか。なんだこりゃｗ

…No.114865+書き込みをした人によって削除されました

…No.114866+nが(p以上の素数の積（重複を許す）)+1としたとき
n=2+1で成り立つ外、p≧5でなんか無数に成り立ってねえ？？
とｵﾓﾀが
左様か…

Name名無し20/12/29(火)00:21:29No.114720+
21年11月頃消えます[全て読む]
整数解(x,y)

…No.114721そうだねx1書き込みをした人によって削除されました

…No.114727+(-1,±1)しか思いつかない

…No.114728+プログラムで-10<=x<=10の範囲で探すと
[(-1,-1),(-1,1),(0,-1),(0,1),(3,-11),(3,11)]
が見つかった

…No.114729そうだねx2(2x^2+x)^2 = 4x^4 + 4x^3 + x^2
< 4x^4 + 4x^3 + 4x^2 + 4x + 4 = 4y^2
< 4x^4 + 4x^3 + 5x^2 + 2x + 1 = (2x^2+x+1)^2
(|x| > 3)
だから、x を整数とすると, |x| > 3 では 2y は整数になり得ない
よって整数解は
[(-1,-1),(-1,1),(0,-1),(0,1),(3,-11),(3,11)]
だけ

…No.114730+ちょっプログラムの実行結果が証明扱いなのですか？！

…No.114731そうだねx3>ちょっプログラムの実行結果が証明扱いなのですか？！
-3<=x<=3の範囲で代入すればわかることでしょ

…No.114831+書き込みをした人によって削除されました

Name名無し21/02/02(火)02:02:09No.114818+
21年12月頃消えます[全て読む]
博士じゃないけど量子異常に愛情持って指数定理を語りたい

…No.114819+

よーしパパ洞中制度とウッズホール固定点定理の関係を北白川というより白川以北とーほく論文のノリで語っちゃうぞー

…No.114820+fixed point theoremを固定点定理って呼ぶ人初めて見た

Name名無し21/01/29(金)21:14:16No.114811+
21年12月頃消えます[全て読む]
本文無し

…No.114812+きも

Name名無し21/01/24(日)05:52:38No.114794+
21年12月頃消えます[全て読む]
最近簡単な暗算ができなかったり、馬鹿みたいな間違いをすることが増えた。
簡単な2桁程度の足し算引き算で、繰上り繰り下がりのある計算がわからなくなる
老化によるものと思っていたがひょっとして
電子マネーを使うようになって、買い物のときに財布から出す金額や釣銭の計算を無意識にやっていたのをしなくなったからではないだろうか。

…No.114795+頭に計算機を埋め込んだらいいと思うよ

…No.114796+計算はやらなくなると、鈍るよ。

…No.114797+書き込みをした人によって削除されました

…No.114798+書き込みをした人によって削除されました