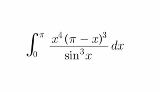
Name名無し20/12/22(火)23:00:51No.114696+
21年11月頃消えます[全て読む]
激ムズ

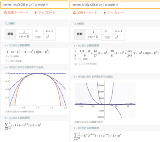
…No.114699+https://ja.wolframalpha.com/input/?i=%E2%88%AB%5B0%2C%CF%80%5D+x%5E4*%28%CF%80-x%29%5E3%2Fsin%28x%29%5E3+dx

…No.114700+Wolfram先生でも数値計算しかしてくれないという…ｗ

…No.114701+9π/8 * (56 π^2 ζ(3) - 62 (10 + π^2) ζ(5) + 635 ζ(7))

…No.114702そうだねx1留数定理を使え、と言われてるだけの問題だよ

…No.114706+>留数定理を使え、と言われてるだけの問題だよ 積分経路どう取るのさ

…No.114707+ 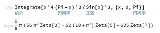No.114701はwolframの計算結果やね

…No.114708+＞全く関係なさそう xが一つ消せるやん そうすればx=π/2で対称だから0→π/2の積分範囲になって… やっぱ解らん

…No.114715+King propertyしてから二項定理で展開すれば、x^n/(sin x)^3を[0,π]で求めればよくて、それは半径1の半円形の積分路を考えることにより、x^2(log x)^n/(1-x^2)^3を[-1,1]で求めることに帰着する、あとはt=x^2と置換してベータ関数の高階偏微分やるだけか

…No.114716+>x^n/(sin x)^3を[0,π]で求めればよくて 発散しない？

…No.114742+>発散しない？ おっと、二項定理で展開できないのか、それなら展開せずにそのまま積分路変更するのが良さそうかな

クエスチョンName名無し20/12/27(日)19:46:12No.114717+
21年11月頃消えます[全て読む]
本文無し

…No.114718そうだねx2tanに関する恒等式 tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) に10°を入れて計算すると tan(3×10°)=tan10°×tan(60°-10°)×tan(60°+10°) tan30°=tan10°×tan50°×tan70° 1/tan70°=tan10°×tan50°×(1/tan30°) tan20°=tan10°×tan50°×tan60° また図より tan(x)=tan10°×tan50°×tan60° となるので x=20° 幾何的な解法は他に委ねる

…No.114719そうだねx3 （細かい角度計算は省略） △BCEが正三角形となるような点Eをとる。CAは△ABCの対称軸なので∠BEA＝∠EBA＝10°∠BDA＝10°＝∠BEAなので四角形BAEDは円に内接する。したがって∠BDE＝180°−∠BAE＝20°∠DBE＝20°＝∠BDEよりEB＝EDよって△ECDはEC＝EDの二等辺三角形となるので他の角から∠EDC＝10°と計算できる。以上より、x＝∠ADE＋∠EDC＝20°

…No.114722+ >tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) これ一般化するとこうなるらしい

…No.114723+>CAは△ABCの対称軸なので∠BEA＝∠EBA＝10° 訂正：△ABC→△EBC

Name名無し20/11/01(日)19:33:13No.114579そうだねx1
9月24日頃消えます[全て読む]
2つの立方体を合わせた立体があります。
1匹のアリが立体の頂点Aを出発して、表面だけを歩きます。
アリがたどり着くのに一番遠い点はどこでしょうか。

…No.114581そうだねx2正方形の一辺の長さを a 頂点Aを原点 正方形の辺の方向に沿って x軸(右方向),y軸(奥方向),z軸(上方向)とすると (3a/4, 3a/4, 2a)の位置

…No.114582+どうやら頂点ではないと！？ 面白いね 19へぇー

…No.114583+表面だけで考えたいから展開図が欲しいな・・・

…No.114584そうだねx2 目的の点は上面のどこか 展開図上で考えると上面のとり方は4パターンあり、それぞれに対応する最短距離の候補がL1〜L4の4つあるmin(L1,L2,L3,L4)を最大値にするような点が求める点B

…No.114598+この問題は最短距離が最大となる点を答えよという意味？ 遠くするだけなら同じところを任意回ぐるぐる回れば良いわけやし…

…No.114599+展開図上の直線は 実際の立体表面の測地線に必ずなる んでしたっけ…

…No.114714そうだねx1 分かりやすそうなサイトがあった http://www.se16.info/js/cuboid.htm

Name名無し20/11/23(月)23:43:50No.114631+
10月16日頃消えます[全て読む]
本文無し

…No.114632+思わずググっちゃったけどエライ問題だなこれ

…No.114633+逆に5%も解ける母集団ってどこだよ

…No.114634+95%って英語圏の決り文句なのか、ぐぐると色々でてくるな 単に多くの人は〜みたいな意味合いだろ

…No.114635+95%ってのは、統計学の信頼区間から来ているんだろ？

…No.114694+数学五輪の過去問や！

…No.114703+書き込みをした人によって削除されました

…No.114704+リンゴっぽいのが女性自身 バナナとパイナップルっぽいのが男性自身 交尾しない分子 交尾した分母 交尾しても1つしか増えないので解は４

…No.114705+メスは多くのオスと交尾しても生まれる子は１

…No.114713+>数学五輪の過去問や！ 数オリでもこんなの出しちゃダメだと思う

Name名無し20/10/31(土)23:50:39No.114574+
9月23日頃消えます[全て読む]
本文無し

…No.114575そうだねx4答えなし！ 和の最上位桁Ｃが１なのは明らか。 そうすると、加えられる数の最上位桁のＡは９でなければならない。（それ以下だと繰り上がりが発生しない） すると百の位のＢが８しかありえない。（それ以下だと繰り上がりが発生しない） 百の位を考えると、８＋１＝９になって良さそうだが、それだと繰り上がりが発生せず、十の位の和の繰り上がりがあるはずだが、そうなると８＋９＋１＝１０となって、百の位が０になるからＡ＝０となって矛盾

…No.114576+条件を緩和して先頭の桁に0がくる事と違う文字に同じ数字を入れる事を認許すとやっと A=B=C=D=0 が解になる 10進法以外で考えた場合も同様

…No.114577+D=-170とするのはダメなのかい？

…No.114580+どこかのBを13に分解して…という手を考えたけど無理だった

…No.114600そうだねx2一部界隈で正答率100%の問題だった…

…No.114601+ギンガマンかよ

…No.114604そうだねx2ガンガン　ギギン　ギンガマン　か 懐かし

…No.114678+ロマンチック　止・め・て

Name名無し20/12/06(日)10:10:00No.114671+
10月29日頃消えます[全て読む]
「y=x^(2n) (n→∞）」
のグラフを数学的に正しく表記するにはどうすればよいか
画像はwindows10の電卓による
y=x^1000
のグラフ
ついでに「y=x^(2n)」を上付き文字で表示する方法を教えてください
いろいろ試したけどうまくいかない・・

…No.114672+電卓のアプリは数値計算できないからなのでは？ そういうのは WolframAlfa でやらせようぜ…と思ったが3Dのグラフが出るな

…No.114673+数値計算じゃなく、式計算ね

…No.114674+y = x²ⁿ

…No.114675+↑記述方法をご教示いただきたく

…No.114676+>No.114675 https://en.wikipedia.org/wiki/Unicode_subscripts_and_superscripts

Name名無し20/11/29(日)22:37:54No.114644+
10月22日頃消えます[全て読む]
ここに3つの箱があります。
ある箱にはリンゴだけ、別の箱にはミカンだけ、さらに別の箱にはリンゴとミカンの両方が入っています。
箱には中身を示すラベルが貼ってありますが、どれも正しくないとのことです。
どれか1つの箱から1つだけ果物を取り出して見て、3つの箱の中身を正しく当てることができるでしょうか。

…No.114651+>どれか1つの箱から1つだけ果物を取り出して見て、 たまたま2つの果物が両方入っている箱に行き当たったらどうするんじゃ……

…No.114652+>たまたま2つの果物が両方入っている箱に行き当たったら ・あからさまに他より重いので持ったらわかる ・箱開けなくても振ったらわかる

…No.114653+書き込みをした人によって削除されました

…No.114654+>・あからさまに他より重いので持ったらわかる >・箱開けなくても振ったらわかる 問題文のどこにも「箱に絵の果物が1個ずつ入っている」とは書いていない 箱詰めになっていたらそれでは分からない

…No.114662+実は問題無い？ リンゴ＋ミカン、のラベルの箱から1個果物を取り出した結果がリンゴだったら、 元の箱の中身はリンゴ1個でしか有り得ぬ、 同じく、ミカンだった場合はミカン1個でしか有り得ない

…No.114663+背理背理フレ背理ほー

…No.114664+組み合わせが具体的に列挙可能なサイズの有限集合だから 別に背理法でも誰も文句は言わないはず…

…No.114665+書き込みをした人によって削除されました

…No.114666+書き込みをした人によって削除されました

…No.114667+書き込みをした人によって削除されました

Name名無し20/11/12(木)00:36:52No.114611+
10月04日頃消えます[全て読む]
本文無し

…No.114612そうだねx3（10+20+24）÷2=27kg

…No.114613+下の白い四角も含めろよ

…No.114614+三角の上に丸が乗るのはバランス的におかしいから浮いているのでは ▲=20kg、■=4kg、●=6kgで？=30kg

…No.114619+>三角の上に丸が乗るのはバランス的におかしいから浮いているのでは 上から見てるのでは？

…No.114620+>下の白い四角も含めろよ 左側の線と数字や文字や記号を入れないの、おかしくないですかぁ？

…No.114630+重量ではなくて質量を問題にしているだけかもしれん

…No.114638そうだねx2〇3 △17 □7

…No.114643そうだねx1大きさを見たところそんな大きな重量差があるとは思えない。 どこかに間違いがある。

Name名無し20/11/04(水)15:32:08No.114586+
9月27日頃消えます[全て読む]
解き方教えて

…No.114588+もとの4桁の数をNとする。(1000 <= N <= 9999) Nの各位の数字を合計した数字をxとする。(1+0+0+0 <= x <= 9+9+9+9 つまり 1 <= x <= 36) 例えばx=10の場合、N=x^3=1000でないといけないが、Nの各位を合計しても10にならない。 x=11の場合、N=x^3=1331でないといけないが、Nの各位を合計しても11にならない。 こんな感じで虱潰しに調べていくのでは。

…No.114590そうだねx1自然数 a の各桁の和を S(a)、ある4桁の整数 x と2以上の整数 n を用いて {S(x)}^n = x …(1) が成立するとする n≠2　…(2)なぜならば(1)より x = {S(x)}^2 ≦ 36^2 < 1999 となるので S(x) ≦ S(1999) = 28 再び(1)を用いると x = {S(x)}^2 ≦ 28^2 < 1000 となって x が4桁であることに矛盾 S(x)が3の倍数ならばS(x)は9の倍数…(3)　なぜならば(1)より S(x) が3の倍数ならば右辺 x が9の倍数となるので倍数判定法から S(x) も9の倍数 x, 及び S(x)の一の位は0ではない…(4)　なぜならば S(x) の一の位が0であれば (1),(2) より x は 10^3 を因数に含むこととなり、x が4桁の整数であることと合わせると S(x)<10 となり矛盾 逆に S(x) の一の位が0でなければ(1)の左辺は2あるいは5の因数を含まないので右辺 x の一の位も0にならない S(x)≠2,4,5…(5)　詳しくは省略するが(4)及び2,4,5の倍数判定法から適合する数がないことがすぐに導ける (1)〜(5)を踏まえて可能性が残る(n,S(x))の組は (3,11)(3,13)(3,14)(3,16)(3,17)(3,18)(3,19)(4,7)(4,8)(4,9) あとは個々計算して調べると(3,17)(3,18)(4,7)が適合するので答えは 17^3=4913, 18^3=5832, 7^4=2401

…No.114591+ ありがとうございます この問題も解いてください

…No.114592+とりあえず最初と最後の数字が1と2になりそうな気がする

…No.114593そうだねx21番目だけを空けて残りを4つずつの塊にする 5番目だけを空けて残りを4つずつの塊にする 9番目だけを空けて残りを4つずつの塊にする 13番目だけを空けて残りを4つずつの塊にする 17番目だけを空けて残りを4つずつの塊にする の5パターンを考えると4つの組が100以上でそれぞれ別の正整数が入る事から17個の整数の総和の最小値が405以上である事はわかる 総和が405になるパターンは数の選び方並べ方によって複数あるが　例えば次の通り なお4つずつで改行を入れながら考えると作り易いと思ったのであえて改行をそのまま残している 1,30,31,38, 2,29,32,37, 3,28,33,36, 4,27,34,35, 5

…No.114602+ ありがとうございます この問題も解いてください

…No.114603そうだねx1(1)2の倍数は21個 偶数1つあたり7個の2の倍数が作れるので、偶数は3つある ⇒取り除いたのは偶数 (2)4の倍数は12個 一の位が2or6→十の位が奇数＝各5通り 一の位が4or8→十の位が偶数＝各2通り 5*2+2=12で条件をみたす ⇒取り除いたのは4or8 (3)7の倍数は8個 作れる7の倍数11個(14,21,28,35,42,49,56,63,84,91,98)のうち 4を含むものが4個、8を含むものが3個なので 取り除いた数字は8

複素関数のテーラー展開Nameあすなろ20/10/29(木)07:52:19No.114559+
9月20日頃消えます[全て読む]
　関数論を再勉強中です。細かなことはほとんど忘れています（笑）。

　1/z(z-2) と 1/z(z+2)を z = 1 でテーラー展開せよ。また、それはどのような範囲で成立するか？

　参考書の似たような問題を見よう見まねで解きましたが、間違いないでしょうか。

…No.114561+とりあえず、WolframAlpha で計算させると全く違うグラフが出力されるんだけど…

…No.114563+少なくとも俺は同じ手順で同じ答えが出たし Wolfram Alphaでも同じ結果が得られた

…No.114564+じゃ、その出力画像でも出して！

…No.114571+ >No.114564