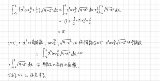07日14:09頃消えます[全て読む]
数学あきたちは得意なんでしょこれ
自己申告でいいけど素手で何十秒くらいで解けちゃうのこのスレは古いので、もうすぐ消えます。

…	>理論が完成してれば追試する必要はないだろ 理論が（形式的に）完成したことと、その理論が正しいこととは別。 当然検証はしないといかんよ。 未だに角の三等分家みたいなのがいるわけだし。

…

>No.112081 苦情はNo.112009に >No.112082 No.112081の意味での最小手数すなわち任意の出題を解ける最小の手数（神の手数）の下限が 20手であることあ1995年にわかっていた >1992年にディク・T・ウィンター(Dik T. Winter)は、スーパーフリップからの復元が20手でできることを確認した。 >1995年にマイケル・レイド(Michael Reid)は、この配置からの復元に20手かかることを示した。 >この手順は1995年にレイドによって発見され、ジェリー・ブライアン(Jerry Bryan)によって最小手数と証明された。 で、上限が20であることも（エレファントな証明でだが）証明されたのだから、 神の手数は証明に間違いでもない限り20で確定

…	つなみに解決したのは2010年8月11日ごろらしい https://science.srad.jp/story/10/08/11/0044228/

…	ルービックキューブの最初の回し方は(x軸3通りx2)+(y軸3通りx2)+(z軸3通りx2)=18通り 2手目以降は15通り（同じ面を続けて回さないため） n手目の可能な配置の上限は 18×15n-1通り (18+18×15+…+18×1515)＜全配置＜(18+18×15+…+18×1516) より17手以上かかる配置が存在することが分かる 対面を回転させる手順は手順前後が可能であることを考慮すると+1なので18手以上かかる配置が存在することが分かる ということで19手か20手のいずれかであることは間違いない

…	>2010年8月11日ごろらしい あぁ、なるほどそこで神の数は２０が確定ってことね。 >No.112081の意味での最小手数すなわち任意の出題を解ける最小の手数（神の手数）の下限が 20手であることあ1995年にわかっていた ちなみにこっちは専門外だけど知ってた。だから質問しただけだよ。

…	>数学あき あきってなんですか？

…	それを理解するためには としあき を理解しないといけない

…	どんなパターンでも20手以内に揃えられるってことですか？

…	20手で生成できる配置パターンは18x15^20-1通り これですべての配置パターンを網羅できる ということだから逆算すればどの配置からでも必ず１〜20手で揃う

…

もはや何でもあり

9月29日頃消えます[全て読む]
これから、あるクラスの中に少女を集める。

クラスの中に、同じ誕生日の少女が2人（以上）いる確率を50%以上にしたい。

何人の少女を集めればいいだろうか？

23人
78人
183人
365人

※閏年や双子は考えないものとする

…	任意の月日に生まれる確率も均等てのが条件だな

…	(364/365)*(363/365)*・・・*((366-n)/365)<0.5

…	https://ja.wikipedia.org/wiki/%E8%AA%95%E7%94%9F%E6%97%A5%E3%81%AE%E3%83%91%E3%83%A9%E3%83%89%E3%83%83%E3%82%AF%E3%82%B9#/media/File:Birthday_Paradox.svg

…	双子を一組入れればいい

14日18:42頃消えます[全て読む]
単位円周上の6点を図のように線分で結んで作られる三角形の面積(赤い部分)を弧長の比で求めたいんだけど高校数学の範疇でできる？

…	方べきと連立方程式で出来そうな気がしそうだけど出来なかった

…	円の中心を原点に、円周上の一点を(1,0)へ持ってくるように合同変換した後 弧長の比から偏角、偏角から各点の座標を求める あとは交点を求めるのに三つ連立方程式解いて、交点の座標から三角形の面積がわかる このプロセスで解けると思うんだが計算が...

…	例えばさ、スレ画の点a,b,d,eをそのまま固定しておいて、線分cfを単位円の中心について回転させると赤塗りの面積はどうなる？ 仮に３つの弧長の比だけで面積が一意的に決まるのなら、それぞれの線分を円の中心に対して適宜に回転させて、例えばb=c,e=dまで動かしても一緒だよね？

…	もっと言えば、 「スレ画の点a,b,d,eをそのまま固定しておいて、線分cfを単位円の中心について回転させる」 てのをやれば、（赤ぬりの）三角形の２つの角が変わっちゃうよね。

…	弦の長さじゃなくて、弧の長さじゃないの？

…	あそうか、ad,be,cfの線分比だと読み違えてた。

…	となると、弧長の比は一般には６つの数の比になる訳？

…	そうなんじゃないかな

…	とりあえず基本的な性質

…	こういう感じでせっせと計算すれば答えが出そうだけど 大変なのでまだ出来てない

13日23:14頃消えます[全て読む]
たまには数式でもUPして見る

…

本文無し

…

本文無し

…

本文無し

…	MITであったなこんなパスワード

…

こんな感じで解く

…

解答は

…	みんな関数系アプリで自動計算で答えは出るけどねえ

…	数学板でむかし拾った画像

…	>No.112045 log_e(55)=4.00733318523247091… なんだろうけど、いいのか？ g=10 と 11 の所が分からん！ 16進法で 0b = 11 なのかいな？

…	重力加速度　g=9.8m/s^2　かな いい加減な時計という事で・・・

問題

15日17:18頃消えます[全て読む]
誰か解いてください

…	157 あるいは 79 ○=1 △=3 □=4 横並びが足し算、縦並びがかけ算 図を囲むのが累乗 累乗の順番が不明なので答えを２つ書いた。

…	ご回答ありがとうございます。 私も157になりました。

…	3^1^4 をどう解釈するかで２通りあるぞ。 (3^1)^4 だろうか 3^(1^4) だろうか。 横式だと普通は前者だろうが、図形表示だとわからないよね。

…	△と△＝27だから3、そして累乗 a≠bでa^b＝4だから1と4 あとはノリで

07日22:10頃消えます[全て読む]
ある日、午前中に雪が降り始めた。
雪はつねに一定のペースで降る。

除雪車が正午（AM12時）ぴったりに動き出し、1時間で2マイルの除雪を完了し、さらに1時間で1マイルの除雪を完了した。

雪はいつ降り始めた？このスレは古いので、もうすぐ消えます。

…	スレッドを立てた人によって削除されました

…	突っ込みどころが多すぎるけど 作者の意図をくみ取って素直に解答すれば 午前11：43頃だな

…	すごいな ちなみに正解は 午前11時23分 微分積分対数を駆使した結果 正午から0.618時間前に雪は降り始めた。 という答えになる らしい

…	手の付けどころすらわからない アプローチを思いつくだけで非凡だなーと思う

…	>という答えになる >らしい 今回は素直に分からない上でスレ立ててるので認めてやる

…	積り始めている雪の積もり続ける量と除雪できる量をグラフに出来ないかな

…	除雪車が走る速度は積雪量に反比例するってことだろ

…	>除雪車が走る速度は積雪量に反比例するってことだろ そこまでくらいならバカなオレにもわかるのでドヤ顔すんな

…	雪が積もってなければ光速を超える除雪車やべぇｗｗｗ 12〜13時の間に進んだ距離 = 2*(13〜14時の間に進んだ距離) 雪が降り始めてからt時間後が13時とすると log(t)-log(t-1)=2(log(t+1)-log(t)) 計算するとt^2-t-1=0 2次方程式といて、13-t時を求めればいい

…	↑ 端的 エレガント 引くのは12時からだけど

13:04頃消えます[全て読む]
同量の1リットルの水を沸かすのに
電気（電熱コンロやIHコンロ）、ガス（LPやプロパン）、灯油（灯油コンロ）のうち
どれが一番安上がり？
今スレ画で手軽なのは良いんだけどボンベ1本100円でずっと使うには高いのでこのスレは古いので、もうすぐ消えます。

…	スレッドを立てた人によって削除されました

…	板違いは黙ってdel

…	手でこすって沸かすのが一番安いよ

…	富士山頂だと気圧が低いので 低い温度で沸騰するよ 山頂には電気コンロや都市ガスは持っていけないから 灯油コンロかスレ画ということになるな

…	本気でマズそう https://www.youtube.com/watch?v=YfZ4iPyMOL0 長期登山だと圧力鍋で調理するって話もあるね