ナンジョウユキヤ
11月25日頃消えます[全て読む]
サクジョ

11月21日頃消えます[全て読む]
0以外のxに対してxとtanx(rad)がともに有理数になることってあるの？

…	ない tan1(rad)が無理数だから

…	tan1(rad)が無理数だとしても加法定理による四則演算の結果無理数の項が消えるかどうかわからない… 詳しい人説明してくれ

…	リンデマンの定理というのがあるらしいです

delete

11月20日頃消えます[全て読む]
life or dead

…

A217570

10月31日頃消えます[全て読む]
1-6の目が出る確率が均等でない6面サイコロがある。
どれか1つの目が20%、その他の目がそれぞれ16%の確率で出るが、見た目では判別できない。

20%の確率で出る目を言い当てることが出来たら100万円を貰えるが、外した場合は100万円を失う。
ただし、サイコロを振って出目を確認する権利を一回1万円で買うことができる。

統計的・期待値的に見て何回振るのが良い？

…	> 外した場合は100万円を失う

…	言い当てるというくらいだから、連続で振られていくサイコロに対して次の出目が２０％だと思った時にだけ言い当てればいいということだよね？ そうじゃなきゃ言い当てるも何も、全ての回で外さないために２０％だと言い続けるしかない どのみち振り続けた結果に対して必ず１００万円が増えたり減ったりするのだから つまりパスも可能だよね？ だけど設問は何回振るのが良いかと聞かれている それと、サイコロの出目を見てから言い当てるなら すべての目を１万払って次々確認していけば、後に全勝だよね？ サイコロを振る前に次に出る目を言い当てるとしたら そもそも１万払って確認する事にどんな意味がありますか？

…	多分勘違いしていると思うんだけど ・どれか1つの目が他の目と比べて出やすいけど、どの目かは分からない ・その目を当てることが出来たら100万円貰える（外したら100万円払わないといけない） ・どの目が出やすいのかを知るために、１万円払ってサイコロを１回振ることが出来る ということじゃないの？

…	>同じ目が出た時点でそれが正解という回答を出す。すなわち最大7回。 これが妥当なんじゃないの？ 最小2回

…	つまりだ、１００回振ったら１００万円かかる。 これでどの目が２０％なのかが確実に分かるのならば、 それを言い当てて１００万円ゲットするから±０円になる。 ただし、１００回程度じゃ確実に２０％の目を当てれるとは限らないし、 もっと少なくても２０％の目を当てれるかもしれない。 そして、振る回数は自由で好きなタイミングでどの目が２０％なのかを１度だけ言い当てる事が出来る。 その１度に対して当たれば１００万円貰えて、 外れたら１００万円失う。 じゃあ何回振ってから言い当てるのが良いのかを、 統計的・期待値的観点から答えようねという問題。

…	●1回も振らない →正解率16.6…%、賞金の期待値-200/3万 ●1回だけ振って出た目を解答とする →正解率20%、賞金の期待値-60万 1回だけ振れば1万円で期待値が20/3万増えるからプラスになる 2回出るまで振ったときに期待値がどうなるか計算するの面倒だな

…	書き込みをした人によって削除されました

…	この問題は実際にさいころを振って試行した結果を どう解釈するかが関係するから そのときの検定のモデルと有意水準をどう設定するかによって プレイヤーが答えに確証を持つまでに要する費用が変動すうｒから 試行回数も当然変動すうｒから 答えが変わる

…	とわいえなんか超合理的で一意な尤度関数でも考え出せれば 一意に決まるかもしれん そのうち考えるはｱﾃﾞｭｰ

…	と思ったけどこの問題はもういいや

10月26日頃消えます[全て読む]
(4)しか解けない

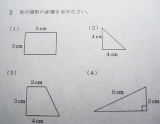
…	じゃあ何故４にだけ直角の記号があるのかね

…	>記号がなければ直角でないという思い込み 長さが見かけの比からずれてるから角度だって違うと考えても別に不思議ではない

…	直線っぽく見える物は直線 という暗黙の了解

…	全ての線が直線だとしても、直角は（４）の１か所だけ

…	>(4)しか解けない ちゃんと右下の立方体の面積を引いたか？

…	立方体である保証が無い

…	(3)の3cmが４cmより長いのですが。。

…

屁理屈スレ

…	4という数字の中央の三角形の面積も足すべきですか？

…	そもそも、紙は完全な平面じゃないので ユークリッド幾何学で計算できないだろ

17日19:03頃消えます[全て読む]
そうかな？

…	No.112118の続きだけど、高校のころ修学旅行か何かで東京に行ったんだが、グループの一人が「友達に会いたいから」と言って別行動したんだよね。 俺らは東京なんてどこ行ったらいいかわかんないから、どこかのデパートのビルの誰もいない非常階段の踊り場で 田舎者らしく座り込んでダベってたら、なんと1日別行動してたはずの一人にばったりと会った。 そんな東京に無数にあるビルの中の誰も来ない非常階段なんかで出会ったりするか？探したって会えないだろｗ あれも今までの人生で不思議な出来事の1、2位に入る。

…	蛋白質等々の塊に宿った魂が 曲がりなりにも平和に生きて活動してることのあり得ない不思議さ

…	そんなレベルの話、世の中の何%が経験していると思うんだ？ 珍しいがありふれてるだろ。

…	>珍しいがありふれてるだろ。 ｗ

…	ここでしか買えないもの がたくさんある世界

…	唯一絶対の神 がたくさんいる不思議な世界

…	よっちゃんいか4連続で当たりがでた

…	山本リンダが楽天・三木谷社長と接触事故

…

119年前にフィルム撮影された皆既日食の動画を英国・王立天文学会と英国映画協会(BFI)が公開した(王立天文学会のニュース記事、The Verge、SlashGear、 YouTube)。 動画は1900年5月28日、英国天文学協会の調査旅行に同行したマジシャンで映画製作者のネビル・マスケリン(グリニッジ天文台5代目責任者で天文学者のネビル・マスケリンとは別人)が米国・ノースカロライナで撮影したもの。皆既日食の撮影は容易ではなく、マスケリンは特製の望遠アダプターをカメラに取り付けて撮影したそうだ。マスケリンは1898年にもインドで日食の写真撮影に成功しているが、帰路でフィルムが盗まれてしまったという。

…	盗んだフィルムは今頃どこにあるんだろうね

10月26日頃消えます[全て読む]
この計算はおかしい

07日12:26頃消えます[全て読む]
スミスさんには子供が2人いる。
1人は火曜日に生まれた女の子です。
では、2人とも女の子である確率は？

※男女が生まれる確率はそれぞれ50%とする


確率ってのは奥が深いこのスレは古いので、もうすぐ消えます。

…	確率ってのは奥が深い♡

…	書き込みをした人によって削除されました

…

スレ文の >※男女が生まれる確率はそれぞれ50%とする という条件は、曜日の数とは無関係に定義できる（P(xが女|xが生まれた)=0.5の意味 にもかかわらずNo.112002の回答は、明らかに「1週間が7日間」という曜日の数に依存している 例えば1週間が8日と定められた別の天体では、スレ題の答えは違う確率になるというわけや ここらで普通何かおかしいと気づかねばおかしい ぶっちゃけ、No.112002は重複数え上げを避ける目的でか「- 「A=4、B=4」(1通り)」 という操作を行っているが、これが誤り。それで避けられたのは重複ではナイ！ カードを2回引いたとき確率1/(14^2)で生じるべき事象を恣意的に削ってしまっている

…	No.112002式のカードへの置き換えによる正しい計算は次のとおり： 　P(2枚引いたカードのうちどちらかが女) = 3/4 　P({2枚引いたカードのうちどちらかが女} ∩ {2枚引いたカードが両方女}) = 1/4 ∴P(2枚引いたカードの両方が女|2枚引いたカードのうちどちらかが女) = (1/4)/(3/4) = 1/3

…	>確率ってのは奥が深い♡ 人生、生命は未来にあるのであって、過去にはない 未来にこそ、真実があるのであって、過去にはない これまでしてきたことは、これからすることに比べれば重要ではない。 これまで犯してきた過ちは、これから創造するものに比べれば何の意味もない あなたの過ちを赦そう 全ての過ちを赦そう あなたの間違った情熱も赦そう 全てを赦そう 間違った意見も、見当違いの理解も、有害な行動も、自分勝手な決定も赦そう 全てを赦そう

…	馬鹿って言ってる奴が一番馬鹿なんだよ これ小学生でも知ってる豆知識な

…	またお前か だからそんなことないと言ってるだろ お前は賢いよ お前が馬鹿だと思ってるやつよりは劣るけど

…	２人が双子である可能性を考えると ２人とも火曜日に生まれた可能性は若干高くなるような気が

…	>No.112066 男女が生まれる確率はそれぞれ50%というのを 双子は常に同性で生まれるという想定で解釈するならそうなるが そうでなければそうはならない

…	>No.112002 >AとBの組み合わせは、14×14=288通りある。 14×14=196

10月05日頃消えます[全て読む]
百マス積分

…	おおおー なんか役に立ちそう 賢い

…	Wolfram Alpha に入れてみたが、積分不可能なのがいっぱい出てきたぞｗ

…	右の方の各列の測度はもっと一般化してまとめられるよね x^k dx、kは任意 exp(kx)dx、kは任意 とかそんな感じで あとこれ、定積分なら留数定理使った方が早いやつが 多いんだけど、なんでわざわざ不定積分なの？

10月17日頃消えます[全て読む]
2のべきって任意の数字列を含んでたりするかな？