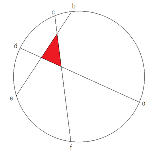
14日18:42頃消えます 単位円周上の6点を図のように線分で結んで作られる三角形の面積(赤い部分)を弧長の比で求めたいんだけど高校数学の範疇でできる？

…	方べきと連立方程式で出来そうな気がしそうだけど出来なかった

…	円の中心を原点に、円周上の一点を(1,0)へ持ってくるように合同変換した後 弧長の比から偏角、偏角から各点の座標を求める あとは交点を求めるのに三つ連立方程式解いて、交点の座標から三角形の面積がわかる このプロセスで解けると思うんだが計算が...

…	例えばさ、スレ画の点a,b,d,eをそのまま固定しておいて、線分cfを単位円の中心について回転させると赤塗りの面積はどうなる？ 仮に３つの弧長の比だけで面積が一意的に決まるのなら、それぞれの線分を円の中心に対して適宜に回転させて、例えばb=c,e=dまで動かしても一緒だよね？

…	もっと言えば、 「スレ画の点a,b,d,eをそのまま固定しておいて、線分cfを単位円の中心について回転させる」 てのをやれば、（赤ぬりの）三角形の２つの角が変わっちゃうよね。

…	弦の長さじゃなくて、弧の長さじゃないの？

…	あそうか、ad,be,cfの線分比だと読み違えてた。

…	となると、弧長の比は一般には６つの数の比になる訳？

…	そうなんじゃないかな

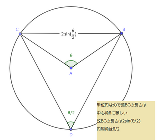…	とりあえず基本的な性質

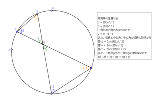…	こういう感じでせっせと計算すれば答えが出そうだけど 大変なのでまだ出来てない