

| …No.116277+ちなみに車検は2年で7万円、駐車場は月5000円です。 車は親のお古なのでタダですが、かうと30〜50万くらいでしょう |
| …No.116287そうだねx1毎日乗るのに借りるとかありえんでしょ 月に一度乗るか乗らんかで買うのもありえんでしょ 完全に人によるので、無意味な設問 |

| …No.116112+>じゃあなんで時間パラメータがtとuの2つあるのは不自然で、 >tだけあるなのが自然と言い切れるんじゃ 虚数時間ってのがあるとも言われとるよ |
| …No.116120+因果関係があるように見えるのは、宇宙がまだ完全な混沌ではないから。 割れた皿はもとに戻らない。紙にインクで書いた文字は勝手には消えない。 でもそれは割れていない皿やまっさらの紙があるからで、最初から土やインクやありとあらゆるものが完全に混ざり合っている世界なら、目に見える変化は何もおきない。 因果関係があるように見えるのは、宇宙が熱的死を迎えるまでのほんの短い間だけなのかも知れない。 |
| …No.116121+お陰で平面の板で3Dゲームできるんだから文句ゆーな |
…No.116122+  中身まで見えてしまうの? |
| …No.116123+4次元の眼があれば何でも見えるよ |
| …No.116124+3次元の目でも2次元を完全に俯瞰することはできないぞ |
…No.116125+  こんな風に目を動かせばいいのでは |
…No.116126+  高次元ブラックホールだと解は一意にならないんだっけ? |
| …No.116131+宇宙の真理を知りたければ哲学科へ行けとインディ・ジョーンズが言っていたじゃないか。 |
| …No.116253+ビッグバンより前は時間の矢が逆向きに流れていたらしい https://gigazine.net/news/20210409-mirror-universe/ |
| …No.116201+>No.116200 君は中卒か? |
| …No.116202+>性質上公開はしないけど結構その辺で似たような問題は見掛けるから知育に力入れてれば簡単に数値上のIQは伸ばせる それも世代を経るごとにIQが徐々に上がっているという事象の説明の一つに挙げられてるね. テストのスコアを鵜呑みにすれば,昔はIQが低くて後から生まれた現代っ子のIQが高くなっている. でもほんとに賢くなってるのかッテ議論ね. |
| …No.116205+>君は中卒か? 私なんか7歳だぞ. |
| …No.116206+>態度とか見られたらジョブズとかアランチューリングとか多動児っぽいのがIQ低く見積もられそうだし 標準以上の水準ならIQスコアなんて大した意味がないんだよ. ランキングなんてまぁ意味がない. 知性ってのは多様で一次元的に並べられるようなそんな単純なもんじゃないよねって反省もあって現代的な指標ができてる. 高IQになってマウントでも取りたいのだったらそれこそ価値がない. |
| …No.116207+IQテストの成績がいい人は探偵の仕事に向いてるのでは? |
| …No.116209+悪童が知能指数高いのは困りものだ。 |
| …No.116210+>IQテストの成績がいい人は探偵の仕事に向いてるのでは? あほ? |
| …No.116211+誰かが考えた法則を逆戻しする能力を計るだけだから 何言ってるかよくわかんない客がくるような受付窓口にはIQ高い人は向いてそう |
| …No.116214+>誰かが考えた法則を逆戻しする能力を計るだけだから >何言ってるかよくわかんない客がくるような受付窓口にはIQ高い人は向いてそう ?ほあ |
| …No.116219+公務員試験の判断推理の事を言っているんだろう |

| …No.116168+書き込みをした人によって削除されました |
| …No.116169そうだねx2クイズスレで答え書くやつってバカなんか? |
| …No.116170そうだねx3かんだい |
| …No.116171+そこか |
| …No.116172+>かんだい 答え見たらここわざと間違ってただけだった |
| …No.116176+>かんだい この棒を使うってことじゃなくて? |
| …No.116208+まあソレが期待されている正答なんだろう 盲点だったわ |

…No.116193+  自分の数学動画を観て恍惚とするルシファー |
| …No.116194+なにこの粘着スレ |
…No.116196+  本文無し |
| …No.116165そうだねx1知るか |
| …No.116180+Malala Yousafzai https://m.facebook.com/naru.sato.73 A005563 しあーみゅーじっく さよならアメリカンぶりー |
…No.116181+  https://www.google.com/amp/s/getnavi.jp/world/578035/%3famp=1 |
| …No.116182+おしまい |
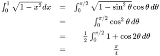
| …No.115843+これの別解を求めよって問題で悩んでいる。 x=tanθ とすると、式が複雑になるし… |
…No.115849+  本文無し |
| …No.116161+四分円の面積とみる |
| …No.116166+部分積分にする |

…No.116135+  これの(2)は,b(n+3)=b(n+1)+b(n)となっています |
| …No.116136+ラメの定理ぐらいしか思い浮かばん https://mathclinic314.com/ラメの定理【ユークリッドの互除法の計算回数】/ |
| …No.115454+>集合、集合の集合、集合の集合の集合、…って階層が型には備わってるって話の方か? こっちはさっきの図では描けなかったが 型Aの部分集合として下位階層の型Sを考えて Sの中の要素a'を想定したら当然それは型Aの要素でもあるので aとa'の写像は型Aの中で問題なく扱えるし前述の通り型Aの外にまたぐと扱えなくなる これならやはりさっき言った通り「型=集合」という認識でよさそう (集合の集合云々だから「大きくなる」と思いきや 部分集合云々の「小さくなる」話になっているのは自分でも引っかかるが) |
| …No.115455+階層があるって話はx∈xみたいなのを避けるために (x : A) ∈ (y : B), (BはAより上位の型) みたいな感じで両辺違う型にしようっていう話だったと思う 部分集合とはまたちょっと違う気がする |
| …No.115457+https://proc-cpuinfo.fixstars.com/2017/05/division-operation-optimization/ グロタンディーク構成 と 負の数の補数表現 と ディラックの海 |
| …No.115458+グロタンディーク構成って要素の圏の一般的な奴らしいけど型と何か関係あるの? |
| …No.115470+5時から男 |
| …No.115471+古めかしいが単純明快で懇切丁寧な論理学の教科書である 前原昭二『記号論理入門』の第8章§1を読んでいたら >∀Fとか∃Fのような<述語に関する限定作用素>をも合わせ考える論理を2階の述語論理といいます。 ><述語の述語>に関する限定作用素を許す3階の述語論理というように、高階の述語論理-あるいは型の理論ともよばれる-というものを一般に考えることもできます。 ってあったのよ この本の第1版は1967年10月15日なんで 当時「高階の述語論理≒型理論」という認識があったということが読み取れる またこの本では第1章§5で述語と性質と概念と条件と命題関数と(内包で書ける)集合を同一視するので つまりは型=述語の述語=(内包で書ける)集合のさらなる(内包で書ける)集合であると考えられる これだと今までの議論と整合的な見解でもある |
| …No.115476+歴史的にはラッセルが集合論のパラドクスを回避するために導入したのが型(タイプ)だけど、ラッセル(とホワイトヘッド)はさらに意味論的パラドクスというのを回避するために階(オーダー)というのも導入した。 でもこれらは定義によっては同じになるので前原先生なんかは同一視して教科書を書きがち。 命題と型を同一視するのは、自然演繹の証明と型付けの導出体系が同型になるからというだけでなく、命題の意味をその証明の集まりと同一視する(BHK解釈)と型っぽくなるという背景もある。 プログラムの表示的意味論というのを与えるとプログラムの型を数学的な集合と対応づけられるようになるよ。 |
| …No.115757+>歴史的にはラッセルが集合論のパラドクスを回避するために導入したのが型(タイプ)だけど、ラッセル(とホワイトヘッド)はさらに意味論的パラドクスというのを回避するために階(オーダー)というのも導入した。 >でもこれらは定義によっては同じになるので前原先生なんかは同一視して教科書を書きがち。 今気づいたけど別物なんですか! 混同してた… |
| …No.116049そうだねx2PM(プリンキピア・マテマティカ)では上でいわれてるように別概念として型と階を導入したけど,同時代のゲーデルらによってより簡便に再定義される.そちらは型と階を実質区別しなくていい. 一応,ゲーデルの定義でも階は論理式の階層のような概念なので型とは違うけれど,内包公理と同様の原理によって集合の一種である型と論理式の性質である階を対応付けている. >型ってなに? ほぼ集合論で言うところのクラス(類)と同じ. でもラッセルのパラドクスのようなものを文法的に排除するために,対象の帰属関係の階層(順序)のようなものを付与して,ひとつ上の階層からの帰属にしか文法的に言及できないように制限した理論を作った. そういう構造付きクラスのことを,あるいはそのクラスに割り振られた階層を見分けるラベルのことを型とよんだ. 階はゲーデル的な型に対応した定義なのか,量化の強さで定義するのかなどでも若干導入が違うし,orderとsortedの用語が歴史的にルーズに使われている. これについては,2階述語論理の標準解釈と非標準解釈やこれに伴うヘンキンの仕事に,そのあたりのモヤモヤを晴らす糸口がある. |
| …No.116133+>>型ってなに? >ほぼ集合論で言うところのクラス(類)と同じ. あーそうか言われてみれば 「こういうものたちがある」というニュアンスだけ見れば 集まりとか真のクラスとか離散圏とかまで単純化出来るな そこから階層などの条件の話もされているが つまりは「特殊な条件の内包である集まり」で まずはそういう観点で見た方がイメージしやすいな… |
| [0] [1] [2] [3] [4] [5] |