Name名無し20/05/06(水)02:32:46No.114024+
12月30日頃消えます[全て読む]
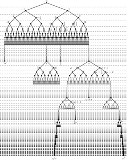
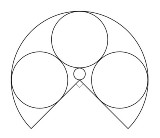
コロナで暇だから和算の問題作りまくった
3/4円の中に同じ大きさの大円3つと小円1つ
小円の半径を1としたとき，3/4円の半径は？

…No.114026+ 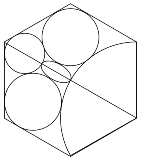正六角形の中に辺の長さを半径とする1/3円 正六角形の2辺と1/3円に接する大円2つ正六角形の2辺と大円2つに接する小円これら3つの円と1/3円に外接する楕円の離心率は？

…No.114027+ 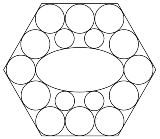正六角形の中に大円12個，楕円，小円4個 小円の半径を1としたとき，正六角形の1辺の長さは？

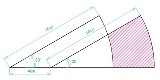
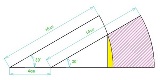
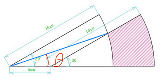
…No.114028+ 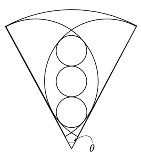中心角θの扇形の中に同じ大きさの半円2つ 半円が重なったところに同じ大きさの円3つcosθ= 3/4，円の半径を1としたとき，扇形の半径は？

…No.114029+やり出すと詰将棋のように時間をかけてしまうので 最初のだけ。

…No.114030+４√２＋６

…No.114031+離心率って習った記憶がない。 天文雑誌では見るけど。

…No.114032+今作る場合、和算問題と数学問題の違いって何なの?

…No.114033+和算は図のような初等幾何の長さや面積、体積を求める問題が多いんじゃないの？ 「証明」は三平方以外興味の範疇外だったみたい。 後期になると、ネタを西洋の惑星軌道などから求めるようになった。 でも、もっぱら近似計算が認められていたからなあ。 微積が無いから、錐体の体積は柱体の体積の1/2.96なんて独自の数値を使っていた。

…No.114089+こういう問題ばっかり解いていると そのうち最密充填問題の上界を下げ始めるのではな いか

…No.114113+ 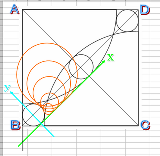三つの円は単位円とする 図のように座標付けする直線y＝x+1+√2放物線y＝x^2/4の交点が正方形の角Aとなる(辺と半径の比率は約０.806らしい)

なんか変な感じName名無し20/05/28(木)04:41:13No.114108+
1月21日頃消えます[全て読む]
Ａ＝Ｂ、Ｃ＝Ｄ
Ａ＋Ｃ＝Ｂ＋Ｄですよね

ポケ＝ポケット、モン＝モンスター
ポケモン＝ポケットモンスター
でも
ポケ盛　＝　ポケット盛　になりません

どんな式を書けば正しいポケ盛になりますか？

…No.114109+>ポケ盛　＝　ポケット盛　になりません ポケ盛のポケは「ポケット」ではなく「ポケモン」を表すものだから

…No.114112+そういやstring の連結演算子で+じゃなくて*が定義されてたのがあったな 順番に意味があるからだとか

Name名無し20/04/03(金)14:27:15No.113776+
11月27日頃消えます[全て読む]
ABC予想スレ
とうとう査読通ったらしいので
https://mainichi.jp/articles/20200403/k00/00m/040/093000c

…No.113865+たかだか:最大が決まっている(無限じゃない) ほとんど:0とか一部の例外を除いて全て

…No.113899+>「たかだか」とか「ほとんど」とか随分ファジーな理論だなと思う 数学用語としてはどちらもwell-definedだけどな。 https://ja.wikipedia.org/wiki/%E9%AB%98%E3%80%85_(%E6%95%B0%E5%AD%A6) https://ja.wikipedia.org/wiki/%E3%81%BB%E3%81%A8%E3%82%93%E3%81%A9_(%E6%95%B0%E5%AD%A6)

…No.113900+「たかだか有限個」ってのは要するに「無限個ではないですよ」ってこったから、数学的にはきっちりしているはず。 ところで、外人にも望月氏を擁護する人がいて、シュルツ氏も押されてきているという話しも…。 門外漢だからどうなるか正直わからん！

…No.113909+決着をつけないと今後数世紀に渡りABC予想絡みの論文の執筆者のモチベに影響する ﾖｶﾝ

…No.113970+でもIUT理論は興味ある ニュートン力学のの微積分とか 量子力学に対するくりこみ理論とかブラ・ケット理論とか なんかそんな感じ

…No.114020+https://www.asahi.com/articles/ASN516HDQN4QULBJ01G.html ABC予想「証明は本当か？」　欧米で論文に異議相次ぐ フィールズ賞を30歳で受賞した若き天才、独ボン大のピーター・ショルツ教授が「論文には深刻で修正不能な飛躍がある」と批判したのを紹介。英国のある数学者は「証明には欠陥があるという見方に変わってきている。あるグループでだけ認められ、他では認められていないのは悪い状況だ」と指摘した。

…No.114021+ちなみに、「たかだか有限個」という言葉は、用語「無限」を避ける為に使われている言葉。 考えて見ると、数学上の多くのパラドックス、ゼノンのパラドックスもラッセルのパラドックスも、実は源泉が無限の実在性から起因している。 「1=0.999…」も直感的には認めたくないが、数学的には認めざるを得ない。微積も高校数学でのものと大学数学でのものが何やらすっきり移行できていない印象。物理では、大学数学が放棄したはずの dx なんてのを無限小が実在するとして扱ってどんどん先にいく。お陰で数学的にはあり得ない微分形式の式を作る物理の人もいる。 これら現代数学が前提とする「実無限」という考えに対して、「可能無限」という立場の人もいて、奥が深く、論争になると面倒って話。

…No.114022+>大学数学が放棄したはずの dx なんてのを無限小が実在するとして扱ってどんどん先にいく。 自分で見て、かなり語弊があるかもｗ 超準解析なんてのもあるし…まあ、この部分は雰囲気でｗ

…No.114101+いかに「無限」と雖も高々有限個の文字数で表せる （思惟の対象とし得る）のであれば 真の無限とは言えんぬ、

…No.114102+リシャールのパラドックス?

Name名無し20/04/16(木)19:46:15No.113894+
12月11日頃消えます[全て読む]
人生ゲーム

…No.114093+結婚しないとダメですか？

…No.114094+ 婚ウェー群、 画像はランダム

…No.114095+インドっぽい

…No.114097+森羅万象はフィボナッチ数であった（適当

Name名無し20/05/21(木)21:16:08No.114090+
1月15日頃消えます[全て読む]
f(f(f(x))) = a^x であるとき f(x) は何でしょうか？

Quoraから転載

…No.114091+Q&Aサイトからの転載に何の意味が?

Name名無し20/04/27(月)12:31:07No.113991+
12月21日頃消えます[全て読む]
非負整数a,b,cの最小公倍数LCM(a,b,c)に対して

　LCM(a,b,c) = a^2 + b^2 + c^2

を満たす組(a,b,c)は無数に存在するでしょうか？

…No.113992+0 <= a <= b <= c <= 500の範囲だと6個あった 0 = 0^2 + 0^2 + 0^2 79560 = 102^2 + 120^2 + 234^2 135720 = 90^2 + 174^2 + 312^2 214020 = 180^2 + 246^2 + 348^2 324360 = 306^2 + 318^2 + 360^2 339300 = 174^2 + 300^2 + 468^2

…No.113993+a, b, cが全部偶数でLCMが20の倍数なのは偶然なんだろうか

…No.113994+78,822,1224とかもそう？

…No.113996+LCM(0, 0, 0) は 0 なのか

…No.113997+簡単なやつだけ証明する 以下、合同式は全てmod 3 (1)a,b,cが全て3の倍数でない場合 a^2≡b^2≡c^2≡1よりLCM(a,b,c)≡0となるが、LCM(a,b,c)は3の倍数にならないので矛盾 (2)a,b,cのうち1つか2つが3の倍数の場合 LCM(a,b,c)は3の倍数となるが、a^2+b^2+c^2≡1or2となり矛盾 以上よりa,b,cは全て3の倍数でLCM(a,b,c)は9の倍数

…No.114001+>No.113992 >No.113994 a,b,cのうちで9の倍数は一つだけなんだな

…No.114007+なんか今日考えてたらa,b,cが6の倍数になることが証明できたんだが何故か忘れてしまった。

Name名無し20/03/27(金)19:48:50No.113728+
11月21日頃消えます[全て読む]
コンピューターでランダム点を打ち込むと
こうなるの何故?

windowsの仕様？

…No.113893+０〜１の間のランダム数字だから 0.2〜0.7は0.5ってすれば集中するような

…No.113907+書き込みをした人によって削除されました

…No.113908+ >とりあえず、スレ画は正規乱数に見えるが？ どういう理由で“正規乱数に見える”のかはワカランが中央付近が濃いからと言うのであればウラムの螺旋だって濃く見えるが・・・

…No.113910+>どういう理由で“正規乱数に見える”のかはワカランが もしかして： 正規数

…No.113911+スレ画が正規乱数かどうかはカイ二乗検定でもやったら わかるんじゃないの 知らんけど

…No.113947+学生の頃に乱数であるか？証明する方法を教わったが 忘れた

…No.113958+>学生の頃に乱数であるか？証明する方法 そんなことできるのか？ 乱数「みたい」なのは作れると思うが 今でも乱数評価は統計的手法でしかできないと思うんだけど

…No.113964+昔、大学生の時数値解析の抗議で πの値をこの乱数表を使って求めた事があった。 3.141592まで正確に出た事がある

…No.113968+>No.113964 >この乱数表 どの乱数表じゃ… >3.141592 標準的なやり方だと https://note.com/shimakaze_soft/n/n9547f5c0bae0 の通りで(4P)/N→πというのを使うが N=10^7ぐらい試行したのでなければ7桁もの一致は単なる偶然の一致と言える （(4P)/Nが比較的少ないNでたまたま良い有理数になっただった) いや知らんけど多分、

…No.113969+書き込みをした人によって削除されました

Name名無し20/04/20(月)02:49:01No.113944+
12月14日頃消えます[全て読む]
数学の自作問題を作りたいのですがどうすればいいでしょうか

…No.113948+何かの決まりがあったら、それを逆に使おうと考えるんだ！ 図形の問題なら、図形の定理を問題に盛り込もうとすると良い。

…No.113952+性質のいい一方向関数は重要だよね。応用分野でとっても。 逆問題とか逆数学まで分野としてあるし。

Name名無し20/04/18(土)17:03:57No.113917+
12月13日頃消えます[全て読む]
半径10cm,中心角30度の扇形が図のように4cm動いた時、
斜線部の面積はだろうか？

…No.113918+失礼、いくらだろうか？のミス

…No.113924+ 黄色の面積を積分で求めたら早いかも。

…No.113926+ √((10sinθ)²︎+(10cosθ-4)²︎)×2×1/2=4×10sinθ×1/2 ⇔√(116-80cosθ)=20sinθ⇔116-80cosθ=400(1-cos²︎θ)⇔cosθ=1+6√2/10→sinθ=√((27-12√2)/100)=(2√6-√3)/10→θ=Arctan((25√3-8√6)/71)(求める面積)=4×10sinθ×1/2+10²︎π×1/12-10²︎π×θ/2π=25π/3+20sinθ-50θ=25π/3+4√6-2√3-50Arctan((25√3-8√6)/71)

…No.113927+>⇔cosθ=1+6√2/10 訂正 cosθ=(1+6√2)/10

…No.113929+半径10cmの円の面積の1/12から 半径6cmの円の面積の1/12を引いた値じゃないの?

…No.113930+半径10cmの円弧を平行移動しても半径6cmの曲率にはならないでしょどう見ても

…No.113939+>(求める面積) >=25π/3+4√6-2√3-50Arctan((25√3-8√6)/71) 25π/3-50Arctan((25√3-8√6)/71)=50Arcsin(1/5) なので (求める面積) =4√6-2√3+50Arcsin(1/5)と表してもいいかも

…No.113940+>>(求める面積) >>=25π/3+4√6-2√3-50Arctan((25√3-8√6)/71) >25π/3-50Arctan((25√3-8√6)/71)=50Arcsin(1/5) なので > >(求める面積) >=4√6-2√3+50Arcsin(1/5)と表してもいいかも なるほど、その方がスッキリしていていいね

Name名無し20/04/10(金)23:01:07No.113872+
12月05日頃消えます[全て読む]
簡単だと思う？

…No.113923+妥当な命題なら大概証明したら真偽がわかるんじゃね…？

…No.113925+>妥当な命題なら大概証明したら真偽がわかるんじゃね…？ つ[連続体仮説]

…No.113928+No.113925がなすべきことは、二次曲線に直線や半直線を含める体系がありえない （必ず矛盾する）ことを示すことであって 選択しだいで結果が変わる複数体系の例を言うことじゃなくね？ 個人的には二次曲線に直線を含めてもいけそうな気がする 円錐の切断の一種とみなすことが可能（ていうか、仮に直線や半直線を含めなければ 円錐の切断方法のごく一部を未定義になる および天体の軌道はすり抜け可能な天体ならば 半直線に成り得るし、

…No.113931+>個人的には二次曲線に直線を含めてもいけそうな気がする 二次曲線に直線を含めてもいけそうなら、四次曲線に直線を含めてもいけそうでは？ そうなると、 >宇宙空間に太陽と、何かの天体があると、天体の軌道は必ず楕円（円）か双曲線か放物線かの、いずれかの二次曲線になるんだよ。 との整合性が担保されなくなる（即ち、"必ず"楕円（円）か双曲線か放物線かのいずれかの二次曲線になる、わけではない為）けど？

…No.113932+書き込みをした人によって削除されました

…No.113933+集合B（直線を含む二次曲線）と集合C（直線を含む四次曲線）が共通部分を有するからといって 集合A（天体の軌道）と集合B（直線を含む二次曲線）がイコールであることに 影響はしない（否定根拠にならない）のでは…

…No.113934+>No.113925がなすべきことは、二次曲線に直線や半直線を含める体系がありえない >（必ず矛盾する）ことを示すことであって選択しだいで結果が変わる複数体系の例を言うことじゃなくね？ No.113925がなすべきことは、引用先のNo.113923の反例について、 選択しだいで結果が変わる複数体系の例を言うことでは？ なぜNo.113925が次曲線に直線や半直線を含める体系がありえない（必ず矛盾する）ことを示さなきゃならないの？ 例えばNo.113925とNo.113906が同一人物というのが明示されているのであればまだ話は分かるけど No.113906についても何も"必ず矛盾する"ことまで言わなくても単に矛盾する可能性があることを示すだけで >天体の軌道は必ず楕円（円）か双曲線か放物線かの、いずれかの二次曲線になる というNo.113882の主張の"必ず"についての反例が成立すると思うけど？

…No.113935+書き込みをした人によって削除されました

…No.113936+>集合B（直線を含む二次曲線）と集合C（直線を含む四次曲線）が共通部分を有するからといって >集合A（天体の軌道）と集合B（直線を含む二次曲線）がイコールであることに >影響はしない（否定根拠にならない）のでは… "必ず〜いずれかの二次曲線になる"との結論に、"四次曲線（特殊な四次曲線である"線分"や"半直線"）といった対象を含めていない"ことが論理的瑕疵だということ

…No.113937+仮にNo.113882の主張が >宇宙空間に太陽と、何かの天体があると、天体の軌道は必ず楕円（円）か双曲線か放物線かの、いずれかの二次曲線、 >もしくは線分か半直線になるんだよ。 であれば（ユークリッド幾何においては）瑕疵は回避できたハズ そもそも直線については概念上二次曲線から排除すべきでないとの前提で主張するならば 同様に概念上四次曲線（四次以上の偶数次曲線）から排除しなければならない前提の理由も主張すべきかと