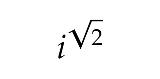
Name名無し19/12/28(土)23:41:58No.113352+
7月31日頃消えます[全て読む]
iの2乗は-1ですが
iの√2乗はいくつでしょうか。
| … | 7Name名無し 19/12/30(月)17:21:56No.113362+theta = pi(2+1/sqrt(2)) cos(theta) + i sin(theta) ってこと? |
| … | 8Name名無し 19/12/31(火)00:17:26No.113363+ 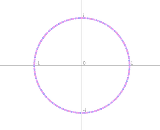 用意していた答えを書きます。 iの偏角は(2 n + 1/2)πのため (ここでnは任意の整数)、 i^(√2) = exp((2√2 n + 1/√2)iπ)である。2√2 は無理数のため、nが異なれば異なる数になる。よって、iの√2乗は複素平面の |z|=1 上に可算無限個存在する。でした。皆様よいお年を。 |
| … | 9Name名無し 20/01/03(金)22:52:13No.113370+非可換トーラスとかに無理やり話し持ってきたいの? |
| … | 10Name名無し 20/01/04(土)02:19:44No.113371+いえ、それは知らないです。 複素数の無理数乗を自分なりに考えた結果です。 もし間違ってたら訂正していただけると助かります。 |
| … | 11Name名無し 20/02/11(火)05:44:26No.113434+>である。2√2 は無理数のため、nが異なれば異なる数になる。 >よって、iの√2乗は複素平面の |z|=1 上に可算無限個存在する。 なるほど面白い 一つしか無いと思ってた |
| … | 12Name名無し 20/02/15(土)02:00:38No.113453+書き込みをした人によって削除されました |
| … | 13Name名無し 20/02/15(土)02:02:44No.113454+ 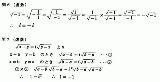 >iの√2乗は複素平面の |z|=1 上に可算無限個存在する。 いやいや、極形式で表現するから見かけ上多価となるだけ(→関数的平方根)。換言すれば、極形式では多価になるから主値を以って一意にする(一価として表現する)必要が出てくる。因みに実軸の負の部分がなぜ正則ではないのかは、平方根関数のリーマン面を見ることで一目瞭然(cross-capとなっている)。だから、画像のような「間違った証明」が出てくる。 |
| … | 14Name名無し 20/02/16(日)22:40:06No.113469+  ぶっちゃけ、平方根に纏わる話題なのですよ。 -1 の平方根についてなのですが、複素数(体を成す二元環、即ち二元体となる「二元数」)においては、i と -i だけなのですよ。というのも、q = a + bi を複素数としてみた場合にその平方(自乗)が -1 に等しいもの(a + bi)^2 = a^2 + 2ab - b^2 = -1 とすると、(1) a^2 - b^2 = -1 ⋀ (2) 2ab = 0 の条件式全てが成り立つことを意味するのですよ。ここで、(2)の方程式を満たすためには、(3) a = 0 ⋁ (4) b = 0のどちらかが必要なのですが、(4)が満たされたとき、a は実数なのに a^2 = -1 を満たさなければならないのはあり得ないので、必然的に (3) a=0 の場合に限られるのですよ。なので、(1) に a = 0 を代入すれば、-(b^2) = -1 、故に b = ±1 となり、「複素数において -1 の平方根は ±i のみ」となるのですよ。(続く) |
| … | 15Name名無し 20/02/16(日)22:42:16No.113470+  (続き) 一方、四元数 q = a + bi + cj + dk では、(5) a^2 - b^2 - c^2 - d^2 = -1、(6) 2ab = 0、(7) 2ac = 0、(8) 2ad = 0 の条件式全てを成り立たせなければならず、同様に、(9) a = 0 ⋀ (10) b^2 + c^2 + d^2 = 1 となるのですよ。これが意味するところは、「四元数において -1 の平方根は f(b,c,d) = b^2 + c^2 + d^2 = 1 の単位球面上に無数に存在する」ということのですよ。結局のところ、「複素数において -1 の平方根は f(a,b) = a^2 + b^2 = 1 の単位円周上に無数に存在する」訳ではない、ということなのですよ。 |
| … | 16Nameベイズ厨 20/03/09(月)21:57:00No.113560+お久しぶりです 八元数ではどうなるんでしょうか |