シストレの途中経過Nameしみじみ20/09/05(土)08:02:23No.114446そうだねx1
7月26日頃消えます[全て読む]
オアンダの結果1

…No.115155+ 結果3

…No.115156+ 結果3

…No.115179+ 結果1

…No.115180+ 結果2

…No.115181+ 結果1

…No.115182+ 結果2

…No.115232+ 結果1

…No.115233+ 結果2

…No.115234+ 結果1

…No.115235+ 結果2

Name名無し20/07/12(日)10:04:04No.114248+
01日10:05頃消えます[全て読む]
イスラエルのスタートアップ企業が、独自の3Dプリンターと食用インクを使って植物由来のステーキ肉を開発したんや。
試食したシェフは、「10人中8人は見分けがつかないだろう」と感想を述べたというんや。
https://www.youtube.com/watch?v=fLpeeUYtW94&feature=emb_title

という記事を見て思った
見分けがつく2人を10人集めたら、全員見分けがつく
ってことなんだろうか？このスレは古いので、もうすぐ消えます。

…No.114521+疑問から馬鹿が滲んでるぞ

…No.114621+今度は人間の細胞を培養して作る人肉ステーキが開発されたとのこと。 いったい未来はどうなってしまうのやら。 http://karapaia.com/archives/52296573.html

…No.114625+アンブロシアプラス

…No.114636そうだねx1その10人は無作為に選んだものとするんじゃないの？

…No.114637+似たようなシェフが10人居て見分けがつけにくいという可能性、

…No.114749+>見分けがつく2人を10人集めたら、全員見分けがつく >ってことなんだろうか？ その理屈で言ったら 見分けがつかない8人を10人集めたら 誰にも見分けがつかないって話になるじゃねえか そんなわけあるかい

…No.114753+最近現れたこういう肉の味は概念としての肉の味だそうだね。 確かに鳥でも豚でも牛でも無いからね。 概念の味を試してみたい。

…No.114754+動物の肉ではないのに何故人間はそれを肉だと感じられるのか… 真円はこの世に無いのに誰しもが頭に真円を思い浮かべることが出来るのと同じ様なものなのかな 肉のイデア？

…No.114762+まさか人口肉でイデアが証明されるとは

…No.114763+書き込みをした人によって削除されました

Name名無し20/12/22(火)23:00:51No.114696+
21年11月頃消えます[全て読む]
激ムズ

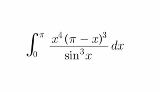
…No.114699+https://ja.wolframalpha.com/input/?i=%E2%88%AB%5B0%2C%CF%80%5D+x%5E4*%28%CF%80-x%29%5E3%2Fsin%28x%29%5E3+dx

…No.114700+Wolfram先生でも数値計算しかしてくれないという…ｗ

…No.114701+9π/8 * (56 π^2 ζ(3) - 62 (10 + π^2) ζ(5) + 635 ζ(7))

…No.114702そうだねx1留数定理を使え、と言われてるだけの問題だよ

…No.114706+>留数定理を使え、と言われてるだけの問題だよ 積分経路どう取るのさ

…No.114707+ 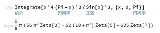No.114701はwolframの計算結果やね

…No.114708+＞全く関係なさそう xが一つ消せるやん そうすればx=π/2で対称だから0→π/2の積分範囲になって… やっぱ解らん

…No.114715+King propertyしてから二項定理で展開すれば、x^n/(sin x)^3を[0,π]で求めればよくて、それは半径1の半円形の積分路を考えることにより、x^2(log x)^n/(1-x^2)^3を[-1,1]で求めることに帰着する、あとはt=x^2と置換してベータ関数の高階偏微分やるだけか

…No.114716+>x^n/(sin x)^3を[0,π]で求めればよくて 発散しない？

…No.114742+>発散しない？ おっと、二項定理で展開できないのか、それなら展開せずにそのまま積分路変更するのが良さそうかな

クエスチョンName名無し20/12/27(日)19:46:12No.114717+
21年11月頃消えます[全て読む]
本文無し

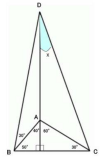
…No.114718そうだねx2tanに関する恒等式 tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) に10°を入れて計算すると tan(3×10°)=tan10°×tan(60°-10°)×tan(60°+10°) tan30°=tan10°×tan50°×tan70° 1/tan70°=tan10°×tan50°×(1/tan30°) tan20°=tan10°×tan50°×tan60° また図より tan(x)=tan10°×tan50°×tan60° となるので x=20° 幾何的な解法は他に委ねる

…No.114719そうだねx3 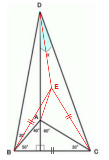（細かい角度計算は省略） △BCEが正三角形となるような点Eをとる。CAは△ABCの対称軸なので∠BEA＝∠EBA＝10°∠BDA＝10°＝∠BEAなので四角形BAEDは円に内接する。したがって∠BDE＝180°−∠BAE＝20°∠DBE＝20°＝∠BDEよりEB＝EDよって△ECDはEC＝EDの二等辺三角形となるので他の角から∠EDC＝10°と計算できる。以上より、x＝∠ADE＋∠EDC＝20°

…No.114722+ 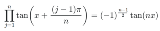>tan(3θ)=tanθ×tan(60°-θ)×tan(60°+θ) これ一般化するとこうなるらしい

…No.114723+>CAは△ABCの対称軸なので∠BEA＝∠EBA＝10° 訂正：△ABC→△EBC

Name名無し20/11/01(日)19:33:13No.114579そうだねx1
9月21日頃消えます[全て読む]
2つの立方体を合わせた立体があります。
1匹のアリが立体の頂点Aを出発して、表面だけを歩きます。
アリがたどり着くのに一番遠い点はどこでしょうか。

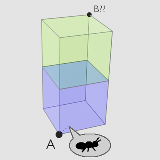
…No.114581そうだねx2正方形の一辺の長さを a 頂点Aを原点 正方形の辺の方向に沿って x軸(右方向),y軸(奥方向),z軸(上方向)とすると (3a/4, 3a/4, 2a)の位置

…No.114582+どうやら頂点ではないと！？ 面白いね 19へぇー

…No.114583+表面だけで考えたいから展開図が欲しいな・・・

…No.114584そうだねx2 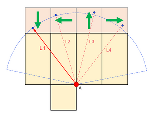目的の点は上面のどこか 展開図上で考えると上面のとり方は4パターンあり、それぞれに対応する最短距離の候補がL1〜L4の4つあるmin(L1,L2,L3,L4)を最大値にするような点が求める点B

…No.114598+この問題は最短距離が最大となる点を答えよという意味？ 遠くするだけなら同じところを任意回ぐるぐる回れば良いわけやし…

…No.114599+展開図上の直線は 実際の立体表面の測地線に必ずなる んでしたっけ…

…No.114714そうだねx1 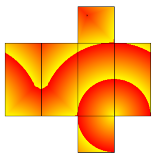分かりやすそうなサイトがあった http://www.se16.info/js/cuboid.htm

Name名無し20/11/23(月)23:43:50No.114631+
21年10月頃消えます[全て読む]
本文無し

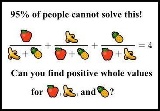
…No.114632+思わずググっちゃったけどエライ問題だなこれ

…No.114633+逆に5%も解ける母集団ってどこだよ

…No.114634+95%って英語圏の決り文句なのか、ぐぐると色々でてくるな 単に多くの人は〜みたいな意味合いだろ

…No.114635+95%ってのは、統計学の信頼区間から来ているんだろ？

…No.114694+数学五輪の過去問や！

…No.114703+書き込みをした人によって削除されました

…No.114704+リンゴっぽいのが女性自身 バナナとパイナップルっぽいのが男性自身 交尾しない分子 交尾した分母 交尾しても1つしか増えないので解は４

…No.114705+メスは多くのオスと交尾しても生まれる子は１

…No.114713+>数学五輪の過去問や！ 数オリでもこんなの出しちゃダメだと思う

Name名無し20/10/31(土)23:50:39No.114574+
9月20日頃消えます[全て読む]
本文無し

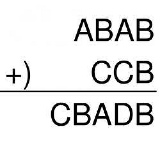
…No.114575そうだねx4答えなし！ 和の最上位桁Ｃが１なのは明らか。 そうすると、加えられる数の最上位桁のＡは９でなければならない。（それ以下だと繰り上がりが発生しない） すると百の位のＢが８しかありえない。（それ以下だと繰り上がりが発生しない） 百の位を考えると、８＋１＝９になって良さそうだが、それだと繰り上がりが発生せず、十の位の和の繰り上がりがあるはずだが、そうなると８＋９＋１＝１０となって、百の位が０になるからＡ＝０となって矛盾

…No.114576+条件を緩和して先頭の桁に0がくる事と違う文字に同じ数字を入れる事を認許すとやっと A=B=C=D=0 が解になる 10進法以外で考えた場合も同様

…No.114577+D=-170とするのはダメなのかい？

…No.114580+どこかのBを13に分解して…という手を考えたけど無理だった

…No.114600そうだねx2一部界隈で正答率100%の問題だった…

…No.114601+ギンガマンかよ

…No.114604そうだねx2ガンガン　ギギン　ギンガマン　か 懐かし

…No.114678+ロマンチック　止・め・て

Name名無し20/12/06(日)10:10:00No.114671+
21年10月頃消えます[全て読む]
「y=x^(2n) (n→∞）」
のグラフを数学的に正しく表記するにはどうすればよいか
画像はwindows10の電卓による
y=x^1000
のグラフ
ついでに「y=x^(2n)」を上付き文字で表示する方法を教えてください
いろいろ試したけどうまくいかない・・

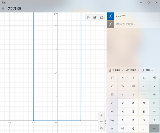
…No.114672+電卓のアプリは数値計算できないからなのでは？ そういうのは WolframAlfa でやらせようぜ…と思ったが3Dのグラフが出るな

…No.114673+数値計算じゃなく、式計算ね

…No.114674+y = x²ⁿ

…No.114675+↑記述方法をご教示いただきたく

…No.114676+>No.114675 https://en.wikipedia.org/wiki/Unicode_subscripts_and_superscripts

Name名無し20/11/29(日)22:37:54No.114644+
21年10月頃消えます[全て読む]
ここに3つの箱があります。
ある箱にはリンゴだけ、別の箱にはミカンだけ、さらに別の箱にはリンゴとミカンの両方が入っています。
箱には中身を示すラベルが貼ってありますが、どれも正しくないとのことです。
どれか1つの箱から1つだけ果物を取り出して見て、3つの箱の中身を正しく当てることができるでしょうか。

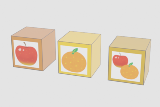
…No.114651+>どれか1つの箱から1つだけ果物を取り出して見て、 たまたま2つの果物が両方入っている箱に行き当たったらどうするんじゃ……

…No.114652+>たまたま2つの果物が両方入っている箱に行き当たったら ・あからさまに他より重いので持ったらわかる ・箱開けなくても振ったらわかる

…No.114653+書き込みをした人によって削除されました

…No.114654+>・あからさまに他より重いので持ったらわかる >・箱開けなくても振ったらわかる 問題文のどこにも「箱に絵の果物が1個ずつ入っている」とは書いていない 箱詰めになっていたらそれでは分からない

…No.114662+実は問題無い？ リンゴ＋ミカン、のラベルの箱から1個果物を取り出した結果がリンゴだったら、 元の箱の中身はリンゴ1個でしか有り得ぬ、 同じく、ミカンだった場合はミカン1個でしか有り得ない

…No.114663+背理背理フレ背理ほー

…No.114664+組み合わせが具体的に列挙可能なサイズの有限集合だから 別に背理法でも誰も文句は言わないはず…

…No.114665+書き込みをした人によって削除されました

…No.114666+書き込みをした人によって削除されました

…No.114667+書き込みをした人によって削除されました

Name名無し20/11/12(木)00:36:52No.114611+
21年10月頃消えます[全て読む]
本文無し

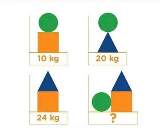
…No.114612そうだねx3（10+20+24）÷2=27kg

…No.114613+下の白い四角も含めろよ

…No.114614+三角の上に丸が乗るのはバランス的におかしいから浮いているのでは ▲=20kg、■=4kg、●=6kgで？=30kg

…No.114619+>三角の上に丸が乗るのはバランス的におかしいから浮いているのでは 上から見てるのでは？

…No.114620+>下の白い四角も含めろよ 左側の線と数字や文字や記号を入れないの、おかしくないですかぁ？

…No.114630+重量ではなくて質量を問題にしているだけかもしれん

…No.114638そうだねx2〇3 △17 □7

…No.114643そうだねx1大きさを見たところそんな大きな重量差があるとは思えない。 どこかに間違いがある。