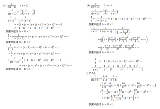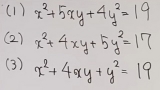Name名無し20/11/04(水)15:32:08No.114586+
21年9月頃消えます[全て読む]
解き方教えて
| …No.114588+もとの4桁の数をNとする。(1000 <= N <= 9999) Nの各位の数字を合計した数字をxとする。(1+0+0+0 <= x <= 9+9+9+9 つまり 1 <= x <= 36) 例えばx=10の場合、N=x^3=1000でないといけないが、Nの各位を合計しても10にならない。 x=11の場合、N=x^3=1331でないといけないが、Nの各位を合計しても11にならない。 こんな感じで虱潰しに調べていくのでは。 |
| …No.114590そうだねx1自然数 a の各桁の和を S(a)、ある4桁の整数 x と2以上の整数 n を用いて {S(x)}^n = x …(1) が成立するとする n≠2 …(2)なぜならば(1)より x = {S(x)}^2 ≦ 36^2 < 1999 となるので S(x) ≦ S(1999) = 28 再び(1)を用いると x = {S(x)}^2 ≦ 28^2 < 1000 となって x が4桁であることに矛盾 S(x)が3の倍数ならばS(x)は9の倍数…(3) なぜならば(1)より S(x) が3の倍数ならば右辺 x が9の倍数となるので倍数判定法から S(x) も9の倍数 x, 及び S(x)の一の位は0ではない…(4) なぜならば S(x) の一の位が0であれば (1),(2) より x は 10^3 を因数に含むこととなり、x が4桁の整数であることと合わせると S(x)<10 となり矛盾 逆に S(x) の一の位が0でなければ(1)の左辺は2あるいは5の因数を含まないので右辺 x の一の位も0にならない S(x)≠2,4,5…(5) 詳しくは省略するが(4)及び2,4,5の倍数判定法から適合する数がないことがすぐに導ける (1)〜(5)を踏まえて可能性が残る(n,S(x))の組は (3,11)(3,13)(3,14)(3,16)(3,17)(3,18)(3,19)(4,7)(4,8)(4,9) あとは個々計算して調べると(3,17)(3,18)(4,7)が適合するので答えは 17^3=4913, 18^3=5832, 7^4=2401 |
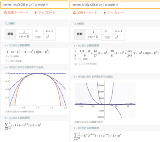
…No.114591+  ありがとうございます この問題も解いてください |
| …No.114592+とりあえず最初と最後の数字が1と2になりそうな気がする |
| …No.114593そうだねx21番目だけを空けて残りを4つずつの塊にする 5番目だけを空けて残りを4つずつの塊にする 9番目だけを空けて残りを4つずつの塊にする 13番目だけを空けて残りを4つずつの塊にする 17番目だけを空けて残りを4つずつの塊にする の5パターンを考えると4つの組が100以上でそれぞれ別の正整数が入る事から17個の整数の総和の最小値が405以上である事はわかる 総和が405になるパターンは数の選び方並べ方によって複数あるが 例えば次の通り なお4つずつで改行を入れながら考えると作り易いと思ったのであえて改行をそのまま残している 1,30,31,38, 2,29,32,37, 3,28,33,36, 4,27,34,35, 5 |
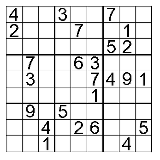
…No.114602+  ありがとうございます この問題も解いてください |
| …No.114603そうだねx1(1)2の倍数は21個 偶数1つあたり7個の2の倍数が作れるので、偶数は3つある ⇒取り除いたのは偶数 (2)4の倍数は12個 一の位が2or6→十の位が奇数=各5通り 一の位が4or8→十の位が偶数=各2通り 5*2+2=12で条件をみたす ⇒取り除いたのは4or8 (3)7の倍数は8個 作れる7の倍数11個(14,21,28,35,42,49,56,63,84,91,98)のうち 4を含むものが4個、8を含むものが3個なので 取り除いた数字は8 |