7月25日頃消えます[全て読む]
ある日、午前中に雪が降り始めた。
雪はつねに一定のペースで降る。

除雪車が正午（AM12時）ぴったりに動き出し、1時間で2マイルの除雪を完了し、さらに1時間で1マイルの除雪を完了した。

雪はいつ降り始めた？

…	スレッドを立てた人によって削除されました

…	突っ込みどころが多すぎるけど 作者の意図をくみ取って素直に解答すれば 午前11：43頃だな

…	すごいな ちなみに正解は 午前11時23分 微分積分対数を駆使した結果 正午から0.618時間前に雪は降り始めた。 という答えになる らしい

…	手の付けどころすらわからない アプローチを思いつくだけで非凡だなーと思う

…	>という答えになる >らしい 今回は素直に分からない上でスレ立ててるので認めてやる

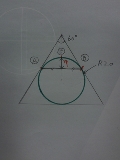
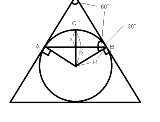
…	積り始めている雪の積もり続ける量と除雪できる量をグラフに出来ないかな

…	除雪車が走る速度は積雪量に反比例するってことだろ

…	>除雪車が走る速度は積雪量に反比例するってことだろ そこまでくらいならバカなオレにもわかるのでドヤ顔すんな

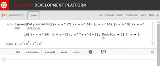
…	雪が積もってなければ光速を超える除雪車やべぇｗｗｗ 12〜13時の間に進んだ距離 = 2*(13〜14時の間に進んだ距離) 雪が降り始めてからt時間後が13時とすると log(t)-log(t-1)=2(log(t+1)-log(t)) 計算するとt^2-t-1=0 2次方程式といて、13-t時を求めればいい

…	↑ 端的 エレガント 引くのは12時からだけど

良問

7月22日頃消えます[全て読む]
1枚だけページが破れた本がある。
破れていないページ番号を合計すると15000になる。
破れたページは何ページ目だろうか？

解法を
小学生にも納得できる様に

…	>これすら君には理解できまいがね ははは なるほど

…	表紙が1ページ目なら解なしだろ。 2ページ目から1ページ目とカウントする本なのか?

…	>2ページ目から1ページ目とカウントする本なのか? 表１表２とか表表紙裏表紙とかいろいろあるんで図解してもらえますか

…

1枚のページの最初の方が奇数ページ、後ろのほうが偶数ページとする。(普通の本はそうなっている) 174ページ目までのページ番号を全部足すと15225となる。 (174+1)x(174/2)=175x87=15225 111ページ目が破れていたら111ページ目と112ページ目がなくなるので残りのページ番号を足すと15002となる。 112ページ目が破れていても111ページ目と112ページ目がなくなるので残りのページ番号を足すと15002となる。 113ページ目が破れていたら113ページ目と114ページ目がなくなるので残りのページ番号を足すと14998となる。 114ページ目が破れていても113ページ目と114ページ目がなくなるので残りのページ番号を足すと14998となる。 1枚だけ破れて残りのページ番号の合計が15000となる解はない。

…	173ページ目で終わってその裏に174ページと書かれていないほんなら25ページ目と26ページ目がやぶれていたら15000になるけど、なんか違和感あるな。

…	>(普通の本はそうなっている) 横レスだけどそういう偶数奇数のどっちがという原則はないよ 1ページ目が右始まり左始まりとか区別して製本屋はどっちにも対応する

…	印刷とページ番号が表だけにあって裏が無い本かもよ？

…	> H - u + u = 1499 答え出てるじゃん

…	>173ページ目で終わってその裏に174ページと書かれていないほん 本当だな ちなみに問題の初出は1994年のインド地方数学オリンピックだそうだ。 https://mindyourdecisions.com/blog/2018/04/19/the-seemingly-impossible-missing-book-pages-puzzle-from-india/

…	スレッドを立てた人によって削除されました

7月22日頃消えます[全て読む]
同量の1リットルの水を沸かすのに
電気（電熱コンロやIHコンロ）、ガス（LPやプロパン）、灯油（灯油コンロ）のうち
どれが一番安上がり？
今スレ画で手軽なのは良いんだけどボンベ1本100円でずっと使うには高いので

…	スレッドを立てた人によって削除されました

…	板違いは黙ってdel

…	手でこすって沸かすのが一番安いよ

…	富士山頂だと気圧が低いので 低い温度で沸騰するよ 山頂には電気コンロや都市ガスは持っていけないから 灯油コンロかスレ画ということになるな

…	本気でマズそう https://www.youtube.com/watch?v=YfZ4iPyMOL0 長期登山だと圧力鍋で調理するって話もあるね

7月16日頃消えます[全て読む]
ボールペンと消しゴムの値段は合わせて110円。
ボールペンは消しゴムより100円高い。
では、消しゴムの値段は？

制限時間１秒

…	>全部自演じゃねーか 認知バイアス >精神分裂症かよクズ 統合失調症

…	>認知バイアス 馬鹿の負け惜しみ >統合失調症 クズの言い訳

…	>なにいってるんだこの馬鹿？ それはみんながオマエに思ってることだバーカ

…	１０円だとずっと思ってた馬鹿がやっと気づいたと思ったらもう燥いじゃって燥いじゃってｗ

…	>１０円だとずっと思ってた馬鹿がやっと気づいたと思ったらもう燥いじゃって燥いじゃってｗ まだ気付いてないんだなー 都合のいい解釈しかできない どうしても都合の悪い事実を認めることができない 認知バイアス その機能障害と性格の悪さ、小心者さ、寂しがりや、甘ったれ、根性なしっぷりが相まって無意味で迷惑な荒らしになる 何をどうしても認知に至らないので、その構ってエネルギーが枯渇するまで無視し続けるしかない ただ、その期間も、常識を凌駕する粘着っぷりなんで、辟易するのみ

…	>まだ気付いてないんだなー 勿体ぶってるけど馬鹿の戯言 悔しいか？ん？１０円くんｗ

…	下敷きはボールペン５本と比べて高くないでちゅ 数まだ数えられないからわかんないでちゅ

…	スレッドを立てた人によって削除されました

…	都合が悪くなるとスレを放置して新たに荒らしスレを立てるクズｗ

…	>都合が悪くなるとスレを放置して新たに荒らしスレを立てるクズｗ という解釈しか出来ないクズ（ｗ

ゴールド系列をつくりたい

6月21日頃消えます[全て読む]
同じ長さのプリファードペアなM系列からGOLD系列が作れる、ということらしいけど、
「プリファードペア」を探すやり方がわかりません。
この論文はシンプルに解説しているように見えるけど、意味が解らない。
実例を挙げて解説してくれませんか。

画像元の論文
www.nict.go.jp/publication/kiho/26/141/Kiho_Vol26_No141_pp863-873.pdf

…	lfsr 1 "1111110" # 7,6,5,4,3,2 lfsr 1 "1111011" # 7,6,5,4,2,1 lfsr 1 "1110111" # 7,6,5,3,2,1 lfsr 1 "1011111" # 7,5,4,3,2,1 lfsr 0 "1100000" # seed=0 lfsr 1 "1110000" # NG tap exit

…

結果。

…	よく分からないけど maximal length sequence prefered pair とかでググってみたらどうでしょうか

…	>No.111331 こういうのってなんのワープロで書いてるの

…	>こういうのってなんのワープロで書いてるの TeXじゃない?

…

てふじゃない

…	このへんが関係あるかも？ https://oshiete.goo.ne.jp/qa/6784882.html

…

↑の教えてgooの回答を参考にしてみると (7,6)にタップを作った場合、α^7+α^6+1=0 またαはGF(128)の生成元だから、α^127=1 t=17のとき、α^tの最小多項式をF(x)とすると F(x)=(x-α^17)(x-α^34)(x-α^68)(x-α^9)(x-α^18)(x-α^36)(x-α^72) これをWolfram Alphaで simplify[polynomialmod[(x-a^17)(x-a^34)(x-a^68)(x-a^9)(x-a^18)(x-a^36)(x-a^72), a^7+a^6+1], a=0] と展開して、modulo 2 で整理すると F(x)=x^7+x^4+x^3+x^2+1=0 なので(7,4,3,2)にタップを作るとプリファードペアになるかも

…	最近はWolfram Open Cloudで無料でノートブックを作れるみたい

…	元の多項式に戻すには t=17 でなく t=15 にすると うまく戻ったけど、これで合っているのだろうか

7月07日頃消えます[全て読む]
モスキート音の実在の証明
死後の世界の実在の証明
は同じロジックで語れる

…	書き込みをした人によって削除されました

…

↑また釣られてる

…	書き込みをした人によって削除されました

…	>やっと釣れた オマエの腕が未熟だってこったｗ

…

つりは忍耐だ

…	>モスキート音の実在の証明 >死後の世界の実在の証明 >は同じロジックで語れる 語れるよ ただ馬鹿にされるけどな

…	>モスキート音の実在の証明 >死後の世界の実在の証明 >は同じロジックで語れる さっさと語れよクズ野郎

…	興味はあるが君と語る気はない

…	>興味はあるが君と語る気はない はい逃げた〜ｗ

…	あ、なんだオマエ >非二元論に興味のある御仁はおらんかね？ このバカかｗ

7月12日頃消えます[全て読む]
国立天文台など世界約８０の研究機関による国際チームは１０日、ブラックホールの撮影に初めて成功したと発表した。ブラックホールは、物理学者アインシュタインの一般相対性理論を基に約１００年前に予言された天体だが、周囲の現象などから間接的に観測することしかできなかった。今回は存在を証明する初の成果となる。

…

ドーナツ食いたい

…	ホーキングがブラックホールは存在しないかもしれないって行ってなかったっけ？

…	ホーキングは白鳥座X1にブラックホールが無い方に科学雑誌1年分を賭けた。BHが有れば研究の成果が実るし、無くても雑誌が只で手に入るので儲けた気になれる。

…	>ホーキングがブラックホールは存在しないかもしれないって行ってなかったっけ？ 行ってはいないと思う

計算式が分かりません…

7月12日頃消えます[全て読む]
数学版の「」の皆様のお知恵をお借りしたいのですがよろしいでしょうか？

以下画像の説明です

Ｒ２．０の円が収まる正三角形があります
正三角形と円の接点ＡとＢを結ぶ直線の中心から
円弧の頂点Ｃを結ぶ直線の値を求める場合の計算式は
どう導き出せばよろしいでしょうか？

プログラムに組み込むのに難儀してます
申し訳ありませんがお願い致します

…	書き込みをした人によって削除されました

…	あ、間違えた（＾＾；

…	こんなもんで 図は半径 R=2.0 の円に外接する正三角形なんですね？ じゃあ求めたい「円弧の頂点Ｃを結ぶ直線の長さ」を x として R - x = R sin30°です。 この関係式は、 円の中心から外接する三角形への接点Ａ、接点Ｂ、 および点Ｃに補助線を３本引くとすぐに出てきます。 なので xについて整理して x = R(1 - sin30°) = 2(1 - 1/2) = 1 ですね。 ※業界によって慣習が違うので 「Ｒ２．０の円」がもし直径2.0の円という意味なら xも1/2にして下さい

…	補助線付きの図で描くと、こんな感じ しかし、Windowsのペイント使いにくいのな（泣）

…	早速の回答ありがとうございます 同僚から聞かれて答えられず困っていたので助かりました 同僚共々御礼申し上げます ＮＣ旋盤のプログラムを作る際使用させて頂きます 改めてありがとうございました

…	なんだまた算数の問題か

…	あっちで負けたからってこっちを荒らすのはやめてください

6月18日頃消えます[全て読む]
このNo.111285の文が正しければ、スレ主は神である。

…	>そうだねx1→自演 そうだね×２になってるね そうだねまで自演してるんだね なんか怖いわｗ

…	No.111681=No.111682 自演してるんだね なんか怖いわｗ 傍から見てるオレには哀れな光景だがな

…	アンカー忘れちゃった 俺が哀れに思うのはNo.111663のことです No.111681とNo.111682　ごめんね

…	>アンカー忘れちゃった >No.111681とNo.111682　ごめんね そんなことで誰が怒るのかと 相変わらず頭の悪い奴だ もう荒らすなよボケ

…	>そんなことで誰が怒るのかと お前が火病ってるじゃん 鏡ないの？ 貧乏〜ｗ

…	No.111685＝ボケ

…	No.111690=No.111685＝ボケ クスクス

…	> No.111691 さすが常駐粘着ミラーリングクズｗ 反応早いな メ欄まで確認するビビリｗ 相変わらず頭の悪い奴だ もう荒らすなよボケ

…	そんなことで誰が怒るのかと 相変わらず頭の悪い奴だ もう荒らすなよボケ

…	> Name 名無し 19/04/01(月)12:24:34 No.111527 del そうだねx3 >ならば、同じロジックで >霊は存在する >に同意できるかね？ ３回自演してるバカ晒しｗ

容積計算方法

7月06日頃消えます[全て読む]
本文無し

…	長物・板物計算が犯しい気がするが気のせいだったようだ