わからんName名無し22/03/21(月)18:53:33No.116741そうだねx1
22年11月頃消えます 本文無し

…No.116742+こんなもん小学生でも解けるだろｗｗｗｗｗ オレには無理だが

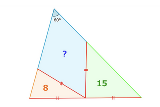
…No.116743+ 俺は数学わからないから式にはできないけど、 三角形8と15とAは同じ長さを持つ二等辺三角形だから面積の比から頂天の角度が出せる(?)すると二等辺三角形Aの頂点の角度も出せる。するとAの面積が出せる(?)。全体の三角形から8と15とAを引けば三角形Bの面積が出せるBとAを足したのが答え。全体の三角形の面積は底辺の長さと全部の角度が出てるから出せると思うｗ

…No.116744+ 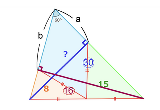大きな三角形の右下の線分は 2b-a 左下の線分は 2a-b。青い長さは √3a 茶色の長さは √3b 青い線の下の面積は 15×2=30 だから、√3b(2b-a)=60茶色の線の下の面積からも同様に √3b(2a-b)=32これを連立させると ab=124/3√3 が出るしたがってこれを使うと大きな三角形の面積は 1/2×2a×2b×sin60°=124/3求める水色の四角形の面積は 124/3-8-15=55/3

…No.116745+なんかおかしいと思ったら連立方程式間違ってるよ >√3b(2b-a)=60 √3a(2b-a)=60 の誤りだと思う これを訂正すると 大きな三角形の面積=48 水色の四角形の面積=25 でさっき計算した結果と合う ところでこれ二次方程式出てくるけど 小学生でも解ける解答は存在するのか？

…No.116746+>No.116744 これはなぜその補助線で直角三角形になるんです？

…No.116747そうだねx2>No.116746 大きい三角形の底辺を直径とする円に内接するから

…No.116748+直感的には「直角三角形の斜辺の中点は、３頂点までの距離が等しい」の逆 証明は中点に円の中心として、任意の弧の上に点を取り、その点から円の直径の端の２点まで線分を２本引くと、中心角と円周角の関係から２本の線分がつくる角は直角になるとでも記述すればよい。

…No.116749そうだねx1>No.116748 なるほど理解

…No.116750+緑は直角三角形？

…No.116755+>No.116750 arccos(1/26)=87.79…°で直角ではない

…No.116756+赤い三角形の面積をS、緑の三角形の面積をTと置いて一般化して解くと 水色の三角形の面積 = (1/3)(S + T + 4√(S^2 + T^2 - S T)) となって多分この数式はこれ以上単純化できないので 解答に2次方程式が出てくることは不可避で小学生では解けないと思われる