Name名無し21/12/17(金)19:56:31No.116213+
22年7月頃消えます 本文無し 削除された記事が7件あります.見る

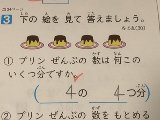
…No.116215+○○　○○　○○ が２この３つぶん ●●●　●●●　●●●　●●● が３この４つぶん で、問題の絵は何と判断できるかって問題だろ？

…No.116217そうだねx14/4だと1個ということに

…No.116218+１個の４つ分でもいいし４個の１つ分でもいいだろうけど算数的には前者なんだろうな． 乗法以前のかけ算を「単位量の乗数（回数）分」で定義するのは線形代数の入り口で，数学の発想がこんな初期の算数の説明の段階で現れているわけだけど，教える側も学ぶ側もよくわからんだろうね． 「単位量の乗数（回数）分」=「いちあたり量のいくつ分」 という表現は，行列の乗法で1行１列行列とスカラーの積，或いは１行１列行列どうしの積．

…No.116220+掛け算順序を固定しての指導は、数学の範疇の問題ではなく、究極的には問題文を適切に読めるかという問題だから国語の問題だよ。 それをこの問題では絵でやっているだけ。

…No.116221そうだねx1長さ×長さが面積の次元になるったりするから 掛け算には足し算の繰り返しを超える意味があるから 出題の国語を真とする場合、 a×bのaとbを交換不可能なケースが出てくる 面積に長さを掛けて体積にすることを考えたらﾜｶﾙ

…No.116222+書き込みをした人によって削除されました

…No.116223+ていうか一時期騒ぎになった 8÷2(2+2) とかも8が面積で2が長さだったら結果として求めるのが 無次元な量なのか面積なのかによって決まるし、 積が和より優先せねばならない理由も正当化される 演算順序はあまねく積の意味に支配されて居うる

…No.116225+>掛け算順序を固定しての指導は、数学の範疇の問題ではなく、究極的には問題文を適切に読めるかという問題だから国語の問題だよ。 その国語の「意味と形式の対応」の意味部分が線形代数の特殊なものとなるように意識して指導に盛り込んでいるのが「かけ算」の水道方式． だから，結局これも数学を意識して指導してるんだよ． 小学校教師多くが水道方式を理解できず，反発も多かったから国語の「構文」論にミニマイズされただけ．

…No.116226+元々子供が構文を理解しているか理解していないかってのの問題だったと思うよ。 まあ数学面で弱いから、水道方式とかで理論化していただけ。 それに、水道方式は直接的に日教組組織率の増大につながった経緯があるから（ホント）、文科省としては継子扱い。

…No.116227+＞8÷2(2+2) これは、省略された乗法の優先がこの場合成立するのか、あるいはこの表記は許されるのかって問題だろｗ 今では一般になっている 8a^4b^3÷4a^3b^2 みたいな計算も普通省略された乗法が優先されて計算するが、この表記を曖昧だとして批判する数学者もいたらしい。 e^x^2 も普通 e^(x^2) と慣例的に解釈されるが、計算は左からという原則からは本当は (e^x)^2 と解釈すべきという人も出かねない曖昧さが残されているわけで…

…No.116229+だから括弧は大事なんだよな． 前後の計算から明らかだとわかる時以外はこういう省略をしちゃいかんってのは理系の解釈一致じゃないか？

…No.116230+>それに、水道方式は直接的に日教組組織率の増大 それも結局は小学校教師が水道方式（というか数学的発想）を理解できずに「偉い先生がいってるから！」ってのを教条的にゴリ押しした結果なんだよ． 水道方式が日教組というカルトを強化したのではなく，元から日教組というカルトが教条主義で「中身より権威」という体質だったから． 数学は「形式と意味」を相互に行き交いするのが大事だが，かつての左巻きは数学を形式の構文論に矮小化してしか理解できなかった．

…No.116231+>文科省としては継子扱い。 もしそうなら，文科省の役人も数学をもとにした算数教育を理解できていないってことになるな． 日教組などが曲解した単なる構文論的水道方式は遠山氏などの理論とは明らかに違う．

…No.116232+文科省もメンツがあるから、一旦対立したんだけど後々その対立がなかったかのように内容をほんのちょっと変えて、全く新しい指導法ですみたいに導入しているんだよ。

…No.116233+＞それも結局は小学校教師が水道方式（というか数学的発想）を理解できずに「偉い先生がいってるから！」ってのを教条的にゴリ押しした結果なんだよ． それは明らかに違うなｗ 単にその方式で指導してみると、効果が出たためってだけ。 まあ、より深い思想をスポイルしているって話しはそのとおりかも知れない。

…No.116234+>No.116227 >(e^x)^2 と解釈すべきという人も出かねない曖昧さが残されているわけで… 無い logをとったら指数の加算と積の関係になるから 積を優先すべき理由が生じる いままで大して問題になっていないのは 指数が無次元量なケースばかりだからかもしれんが 積の意味がそれを要請する （か、指数のlogと通常の加減算の理由なき不統一を甘受せねばならない

…No.116235+>全く新しい指導法ですみたいに導入しているんだよ。 だよね．本質的には変わってないよね． なんであんな論争になったんだろうって感じだ． 時々再燃するけどさ．

…No.116236+それから、ホントに日教組の組織率が上がったのは水道方式のため。日教組が水道方式を支持していたためだ。 文科省の方法では指導効率が上がらなく、日教組の方式では指導効率があがるのだから仕方ない。 これを書いているのは文科省出身の岡本薫ね。Wikipediaには地理学者とあるけど。 ＞logをとったら指数の加算と積の関係になるから ＞積を優先すべき理由が生じる それは分かる。だからこそ「慣習」と書いただろ？原則からは外れているのは明確な事実。

…No.116237+>それは明らかに違うなｗ 単にその方式で指導してみると、効果が出たためってだけ。 それは文科省の言い分か？日教組の言い分か？ なんにせよ大差ないね．

…No.116238+書き込みをした人によって削除されました

…No.116239+>それから、ホントに日教組の組織率が上がったのは水道方式のため。日教組が水道方式を支持していたためだ。 その話は，遠山・銀林先生らの「本来の水道方式」と日教組の教条的教育をごっちゃにしてるからこの話題では意味ないね．

…No.116240+>それから、ホントに日教組の組織率が上がったのは水道方式のため。日教組が水道方式を支持していたためだ。 それをホントに強弁したいなら統計的因果推論で示さないといかんけどね． 交絡や衝突が一切ないことを示せるかい？

…No.116241+＞それは文科省の言い分か？日教組の言い分か？ 元文科省の役人だった岡本さんが実際にそれ書いているよ。わざわざ文科省が敵対していた組織を利する行為をしていたと書いている。 ＞その話は，遠山・銀林先生らの「本来の水道方式」と日教組の教条的教育をごっちゃにしてるからこの話題では意味ないね． そうかも知れないが、関連はある話し。

…No.116242+>元文科省の役人だった岡本さんが実際にそれ書いているよ。 「単なる国語の問題」とミニマイズして構文論として「かけ算はこの順番なんだ〜〜！」って教条的に強制するのが日教組的． 私が先に書いたのは本来の水道方式の意味内容． その対比に日教組の組織率の話なんて関係がない．

…No.116243+加減算より積を優先すべきなのは慣習では無い 1 m^2 + (2 m × 3m) -- OK意味が通る (1 m^2 + 2m) × 3 m -- ナンセンス 単位をどう弄っても無次元量でない限り 加減算の前に次元をそろえる操作が要る == 積が先、加減算はあと

…No.116244+そういう理由他があるから、慣習にしているだけだろ。

…No.116245+＞「単なる国語の問題」とミニマイズして構文論として「かけ算はこの順番なんだ〜〜！」って教条的に強制するのが日教組的． ＞私が先に書いたのは本来の水道方式の意味内容． だから、個々の教師が本質を理解していないって話はまた別な。現場労働者はどうしてもノウハウだけを求めたいし、それを覚えると仕事が捗るってのは魅力的だ。 だれもが、本質を理解して仕事したいと思ってやっているわけでもなし。

…No.116246+>だから、個々の教師が本質を理解していないって話はまた別な。現場労働者はどうしてもノウハウだけを求めたいし、それを覚えると仕事が捗るってのは魅力的だ。 それって私の書いてあることと何ら矛盾しない内容なんだが．

…No.116250+>>(e^x)^2 と解釈すべきという人も出かねない曖昧さが残されているわけで… >無い ソコは違うと思うな． 対数を取る操作は底（指数・対数の）が決まらなければ本来定まらない操作． e^x^2の表記規則を(e^x)^2とe^(x^2)のどちらの略記とするかという問としよう． 底eの対数をとる操作だと解釈を固定した場合， (e^x)^2=e^2x　→　log(2x) e^(x^2) →　log(x^2) なので，乗法とべきの優先順位で形式不易的な齟齬が生じているかのように見える． しかし，これは底をeとしたからであって，前者なら底を(e^x)とするなら齟齬はない． 前者の解釈で対数をとる時に底をeとしてしまう発想は括弧（）があるのにその結合を無視して演算(逆演算）の順序を変えてしまうという不整合を行っている．これは不条理だ．

…No.116251+書き込みをした人によって削除されました

…No.116252+A*B*Cという演算の式があり，結合法則が必ずしも成り立たない場合，(A*B)*CとA*(B*C)の2つの解釈が存在しうるが，どちらか一方が暗黙に慣例であるとするならそちらを略記できるというだけで論理的必然性はない．通常左から計算していくという慣例規則があるが，それを当てはめれば， A*B*C*D*E*F*G…というのは， (…((((((A*B)*C)*D)*E)*F)*G)*… の略記のこと． 指数表記を二項アレイとし，同様に左から計算すると解釈する場合ならば，対数をとる操作という逆演算は括弧の一番外側から行わないと不整合だから右から順次展開していく．そのルールを破っているのだから形式不易的な不整合が起こるのは当たり前といえる． 慣例で指数表記は右から計算していくようになっているので，対数操作という逆演算は左から逆順に展開していくと整合的で，それが暗黙にeを底とする操作と一致する（底がeの指数関数なら）． 類似の現象は線形代数の基礎でもでてくる． 正則行列の積とそれらの逆行列の積は対応するモノ同士の順序が左右逆だろう？ つまり，e^(x^2)の解釈を採用しているのはこの地球文明の慣例といえる．全宇宙でどちらが多数派かはワカラナイが．

…No.116254+>No.116250 >前者の解釈で対数をとる時に底をeとしてしまう発想は（中略）不条理だ． それNo.116234と同じ、、、 指数に多項式が来るケースを考えると状況がはっきりす、 　e^(a + b * c^n)のeを底とする対数 = a + b * c^n a≠0んときとそうでないときで規則を変えたくなかったら b * c^nを先に計算する他ﾅｻｽ さらに 　e^(a + b * c^(d + f * g^n)) とかになってくると規則の統一のうまみがさらに増す この慣例、まさしく必然や……！

…No.116255+書き込みをした人によって削除されました

…No.116256+実際のところ乗算が次元を上げる操作なら、 冪は次元をﾁｮｰ上げる操作 これと「異なる次元のﾌﾞﾂの加減算はできない」を真とするならば、 カッコによる明示が無い場合、多重の冪において何から優先して演算すべきかは確定的に明らか…、 指数が確定せねば冪は確定しないのだ から……

…No.116259そうだねx1「何個のいくつ分」という言い方自体が聞いたこともなく・・・ 本当に正しい日本語なのかと 解釈しようにも想像の域を出ない

…No.116260+確かに！　問題作ってる人物の日本語能力が‥ これじゃ誤解する子供もいるでしょうね 「プリンは一皿にいくつずつ？　お皿はなんまい？」の様な 質問にして、見切れてる次の質問に繋げるイメージなんでしょうけど

…No.116261+よく見て見ろ ４の上にレが付いてるだろ？ ４に個が付いてないから間違いなんだよ

…No.116262そうだねx1＞「何個のいくつ分」という言い方自体が聞いたこともなく・・・ ＞本当に正しい日本語なのかと 専門用語を作って「この言葉の意味はこれですよ」ってやることは普段の授業でも多々あるし、法律でもマスコミでもその他多方面でやっている。 算数だったら午前、午後、正午の扱いが普通の日本語と違う（というか、日常用語がどこか曖昧）。以上以下未満超えるも日常用語とは違った扱いをするときもある。距離は小学校では最短距離の意味だけで固定するが日常用語では違った扱いだ。割合の比べられる量、元にする量は教科書毎で違う表現だったりする。 そんなもんだろ。

…No.116264+>この慣例、まさしく必然や……！ 括弧の入れ方に複数の解釈がある時点で何をどう取り繕っても「必然」ではない． グダグダ言い訳しても無駄．

…No.116267+>指数が確定せねば冪は確定しないのだ 「表記規則が確定せねば演算が確定しない」が正しい． 何をどうこねくり回しても，冪演算を2項アレイ表記とみなした場合には複数の解釈がある． つまりはこれを右結合優先と解釈するのは慣例であって必然ではない． そもそも指数表記を文字の右肩に指数を書くという書き方すら必然ではない． （右肩に置く書き方を左肩に置く書き方に変更すれば，左結合優先で齟齬がなくなる．）

…No.116268+＞本当に正しい日本語なのかと お前さんが「聞いたことがない」ということは日本語として正しいのかどうかとは無関係．

…No.116270+よく分かっとらんみたいだが，結合則が必ずしも成り立たない二項演算において，括弧無しなら3項以上になると解釈依存性の自由度が発生する． 括弧をつけることで紛れなく表現できる複数の（この例では2つの）解釈が存在するなら，それらは括弧を付けた状態の表現が正式なものだ． 括弧を外した状態でどう解釈するのかが慣例かという問いは「括弧なし表記が，どの括弧の位置での解釈の略記とするのか」という話でしか無い． 利便性の状況証拠で補強しても「必然」にはならない．さらに状況証拠に使われている表現のいくつかも慣例だ． どう転んでも「必然」にはならない． あくまで慣例は慣例だ．

…No.116272+書き込みをした人によって削除されました

…No.116273+>カッコによる明示が無い場合、多重の冪において何から優先して演算すべきかは確定的に明らか…、 それは，複数の表現の多義解釈があるという事実の言い換えであって，必然性の証明にはならない． 多義解釈可能な曖昧な表記が存在し，それを略記のままどう確定するのかという問題は，その形式の外部の理論だ． ある形式の表記でAとBという2つの解釈が存在し，曖昧さを排除しなければならない時，AとBのどちらを選ぶべきなのかに必然性はない． どうあがいても無駄． これすら理解できないなら，小学校の国語と算数からやり直したらどうだ？

…No.116274+まぁ，書いてあることの悉くがツッコミどころ満載だ．

…No.116282+書き込みをした人によって削除されました

…No.116283+書き込みをした人によって削除されました

…No.116284+指数に多項式が来るケースを考え合わせると、 指数を先に計算する方が解釈に統一感が出ることはNo.116254に書いた （多項式の中に指数関数が含まれる再帰的なケースと単純な多重冪を共通に扱える さらに追加を述べる。 左から計算するべき(((a^b)^c)^d) というのは a^(b*c*d) に他ならず、 多重冪に見えてじつは単一の冪でしかない。 つまり、a^b^c^dという略記を(((a^b)^c)^d と解釈することで計算が簡易になるような >外部の理論 (>No.116273) が存在するとは大変疑わしい 一方、a^(b^(c^d))は真正の多重冪であってこの別表現は容易には見つからない （単一の冪が次元をﾁｮｰ上げる操作なのに対して、多重冪はﾁｮｰﾁｮｰ上げる操作 限られた略表記をどっちの解釈に割り振るのが合理的か、普通の人にとっては確定的に明らか、

…No.116285+No.116264〜No.116274は一般論を振りかざしてゐるだけで 冪演算の合理的な略記法を論じる観点がすっぽ抜けている 漏れがグダグダ言い訳しているのではなく、No.116264〜No.116274の頭の中がグダグダなのだ

…No.116286+訂正orz ×: 指数関数 〇: 累乗

…No.116292+積分の問題で次のようなものがあった ∫sin(5x+π/2)x dx これは ∫sin｛(5x+π/2)x｝dx　なのか　∫｛sin(5x+π/2)｝x dx　なのか曖昧だ でも、∫sin｛(5x+π/2)x｝dx　は極めて難しい積分になると思える、∫｛sin(5x+π/2)｝x dx は部分積分で何とか解けそうだ。 つまり最初の式は多分 ∫｛sin(5x+π/2)｝x dx ではないかと忖度できる…よおし、そうだとして解こうか！！ というか、こんな曖昧な表現の問題を出すなよｗ おっと、No.116284の話はわかるけど…必然性はないなあ。

…No.116332+>限られた略表記をどっちの解釈に割り振るのが合理的か まだワカランのか？ その合理的か否かって話が慣例だってことだ． 合理性の判断基準は数学的な意味での「一意性」とはかけ離れて曖昧だ． つまり慣例に過ぎない．

…No.116333+>つまり、a^b^c^dという略記を(((a^b)^c)^d と解釈することで計算が簡易になるような >>外部の理論 (>No.116273) >が存在するとは大変疑わしい 全く分かっとらんな．お前さんが言ってるのは「状況証拠による補強」に過ぎない．「必然である」という主張ができる程度の数学の証明になってない． 括弧省略なしの表記で真正に両者を外部の理論なしに区別できるという実例があるのだから，それ自体が「必然である」の反例になっている． そもそも略記は慣例なんだよ． その理由付けが権威だったり合理性だったりするだけだ． そういう外部の意味づけとは無関係（つまりキミが言っている合理性などという補強理由と無関係に）に括弧省略なしの表記では両者を紛れなく区別できている． これが必然ではないという証拠だ．