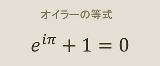
どういうことなのName名無し21/09/07(火)09:06:42No.115887+
3月22日頃消えます e^iπ+1=0だというけど

2.71828^3.14159+1=24.1405823262だというのに何故
0になるんだ？🎵

…No.115888そうだねx1何故iを無視するんだ？

…No.115890+オイラーの公式 e^(iθ)=cosθ+i sinθ に θ=πを代入すると… e^(iπ）=cosπ+i sinπ=-1 となるからな。

…No.115894+wolfram先生によると 2.71828^(3.14159 × i) = -1.0000 + 4.76679 × 10^-6 i だそうだ つまりほぼ -1 になる

…No.115899そうだねx1オイラーの公式がしっくり来ないとしあきは τ (タウ) を使え https://www.youtube.com/watch?v=1jDDfkKKgmc

…No.115903+i=√(-1)を√163に置き換えると e^(π√163) = 262537412640768743.999999999999250072

…No.115908+e^(π√163) のことはラマヌジャンの定数と呼ぶらしいですが ほとんど整数に近いのは何故なんでしょうね

…No.115909そうだねx1 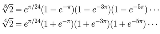j-invariantの特殊値が j((1+√-163)/2) = -640320^3 となることとq=e^(2πiτ)と置いたときのj(τ)のq展開がj(τ) = 1/q + 744 + 196884q + 21493760q^2 +...となることより-640320^3 ≒ -e^(π√163) + 744

…No.115913+ 本文無し

…No.115914+ 本文無し

…No.115917+lnx+γ-Σ[x/k]=r k=1 to x lnx+γ-Σ[x/k]>0 γ>Σ[x/k]-lnx≒0.15　　 γ=Σ[x/k]-lnx+r lnx-Σ[x/k]が増加なのでｒも増加する -0.198556598 -0.181843215 -0.172037558 -0.156094143 -0.15490337

…No.115918+ 本文無し

…No.115919+ 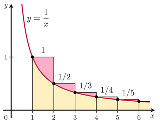γはしたのピンクの部分の面積の総和になります。

…No.115924+変だぞ

…No.115925+ 収束するぞ

…No.115926+ 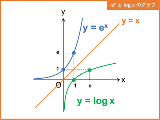e^0.6931471805599453094172321=2 ln2=0.6931471805599453094172321

…No.115927+e^0.7じゃなかったなぁ

…No.115928+ もう大丈夫です。

…No.115929+ 終了です

…No.115986+円周を半径で割ったものをπと定義してたら e^(iπ）=1 だったんだぜ この方が断然美しい 今からでも遅くないから、そう定義しなおして欲しい