Name������21/06/27(��)06:43:43No.115402��������x1
1��11���������܂� �^���ĂȂɁH
�W���Ƃ͈Ⴄ�́H
| �cNo.115403+�R���s���[�^�͒ʏ�A�������������Ȃ��B���̐������ǂꂾ���̑傫���̐������������Ń������[���g���ʂ��ς��B ���̌`���͐F�X�l�����邪�A�`�����Ƃɕϐ����\����͈͂�A���x���ς����Ă��ƁB ���̌`���̂��Ƃ��^�Ƃ������킯���B |
| �cNo.115405+�����Ɛ��w�I�� More mathematically |
| �cNo.115406+�Ⴆ�A���������^�ł�0��1�̑g�ݍ��킹�i�r�b�g�j�̐��Ō^���������Ă���B int16 �Ȃ�16�r�b�g�������萮���B int32 �Ȃ�32�r�b�g�������萮���B int64 �Ȃ�64�r�b�g�������萮���B ���ꂼ�ꈵ���鐮���͈̔͂��Ⴂ�A�r�b�g���������Ȃ�Έ�����͈͂��L���邪�A�������[��H���B ����CPU��64�r�b�g��32�r�b�g�B32�r�b�g�}�V����64�r�b�g�����������ɂ͂�����Ƃ����H�v���K�v�ƂȂ�B unsigned int �Ƃ����^������A����͐��̐��������������Ƃɂ��������^�B������g���ƈ����鐔�͈̔͂��Q�{�ɂȂ邪�����͈����Ȃ��B float , double �Ƃ����̂́A�����������~�w�����Ƃ����Q�̐��ɕ���������������悤�ɂ������́Bdouble��float�̂Q�{�̗e�ʂ��g���A�Q�{�̐��x�Ōv�Z�ł���B ���Ȃ݂ɁA���ۂɂ͂ǂ̂悤�ȃr�b�g�\���ɂȂ��Ă��邩�͋@�킲�ƂɈ���Ă��邪�c���� IEEE754 �̍\���ɂȂ��Ă���͂��B���ꂪ���\���G�Ƃ������A�Ȃ�ł�����`�����̂��[�Ƃ������B�܂��A���͋@�B�Ōv�Z��������ǂˁB |
�cNo.115407+ 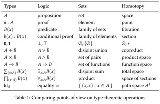 ���₻������������̘b�ł͖����Č^�̌����ƏW���̌����̈Ⴂ���m�肽�� ���������^���_��ZF�����݂����Ȃ̂��Ă���́H |
| �cNo.115408+�^�Ȃ�ăR���s���[�^�̎�����̓s������Ȃ��́H �`���[�����O�̂����}�V���Ɍ^�Ȃ�ĊT�O�Ȃ��ł��� �[���͒��ׂĂȂ����� |
| �cNo.115409+����^���̂̓R���s���[�^�̑O���炠��� �v���O���~���O�ɉ��p����Ă���Ă����ŃR���s���[�^���L�̊T�O����Ȃ� |
| �cNo.115410+�ł��A�R���s���[�^��Ɏ��������^���ĉ��@�ł���S�P�˂���Ȃ����Ȃ��B�����ӂ�Ƃ��A��̂āE�l�̌ܓ��Ƃ����邵�B ����Ȃ��ZF�����n�ƌ����Ă��c |
| �cNo.115411+�Ƃ肠�����R���s���[�^�̘b�͖Y��Ă�����āc |
| �cNo.115412+�X���悪�ǂ��Ȃ������̂�������Ȃ� |
| �cNo.115413+>�R���s���[�^��Ɏ��������^���ĉ��@�ł���S�P�˂���Ȃ����Ȃ��B �����������@�͑S�P�˂���Ȃ��̂ł� |
| �cNo.115414+�^�͏W���Ƃ������������Ȃ�Ȃ��� �����畔���^�Ƃ����a�Ƃ����ςƂ��^�̊��Ƃ��^�̌^�Ƃ����l���邱�Ƃ��ł��� |
| �cNo.115415+�W�����܂��Ă銴�����낤���nj^�ɂ����ďW���ɖ����̂��ĂȂ� |
| �cNo.115416+�R���s���[�^�̎����Ȃ��̌^�̒�`���āc�킩��� �^�̌^�H�R���s���[�^���ƁA�@�B��̂��̌^�ւ̃|�C���^�[�݂����ȃ��c�H�� �^�̊��H�w�肵���^��Ԃ����H ���w���Ƃǂ��Ȃ�H ����������Ɖ��@�̊����`����ƁA�S�P�˂Ȃ�H |
| �cNo.115417��������x11+3��2+2��4�ɂȂ�̂ɂǂ����S�P�˂Ȃ�c�c |
| �cNo.115418+>�^�̌^�H�R���s���[�^���ƁA�@�B��̂��̌^�ւ̃|�C���^�[�݂����ȃ��c�H�� �Ⴆ�� 123 : Int ������ Int : Number �݂����Ȃ̂������Ă��ǂ����Ď����� �v���O���~���O�Ō����ƌ^�N���X�ɑ������銴�����ȁH |
| �cNo.115419+�ǂ������ƌ����ƃJ�C���h�̂��ƂȂ̂��ȁH |
| �cNo.115420+>�^�̊��H�w�肵���^��Ԃ����H ����͂����ɏ���Ă�z���ȁH https://qiita.com/HirotoShioi/items/39fc492401e4dcbc8cba Zero�^��Succ Zero�^, Succ(Succ Zero)�^, ... �ƍ���čs���Č^��"���R��"���������o����炵�� �ōX�ɂ���"���R��"���m�𑫂�Add�^���Ƃ����̂���`�ł���Ƃ� |
| �cNo.115424+���̗������Ԉ���Ă�̂�������� �u�W���̏W���v�̂��Ƃ���Ȃ��������� �u�S�Ă̏W���̏W�܂�v���ӂ��̏W���̂悤�Ɉ����Ɩ��������Russell���ؖ����� ����Russell���u�W���̏W���v�u�W���̏W���̏W���v�ȉ������g���܂���� ����������ł���̂ł͂Ȃ����Ƒ�ĂƂ��Ē������ ���p�ア�낢��ƕ֗��ȕ��@�ł͂������� �u�S�Ă̏W���̏W�܂�v��Ƃ��Ă͎��s�����Ƃ����Ƃ� ���̌�Quine�̌n�������̘H���Łi���q�I��urelements��lj����āj �u�S�Ă̏W���̏W�܂�v��ɐ�������ZFC�����n�Ƃقڑ��F�Ȃ� ���w���T�O���\���ł���NFU�����n��������Ƃ����Ƃ��i�ڂ����˂��j |
| �cNo.115425+>�u�W���̏W���v�̂��Ƃ���Ȃ��������� ����͐^�̃N���X���ēz���Ǝv�� ��Ńp���h�b�N�X���������̂̓J���g�[������Ȃ��������� ���b�Z���̃p���h�b�N�X��R={x| x∉x}�Ɋւ���z �^�͉����l�̉E���ɒ��߂Ƃ��ĕt���Ă銴���̃C���[�W 123 : ���R�� �݂����� ����"���R��"���^ |
| �cNo.115426+>����͐^�̃N���X���ēz���Ǝv�� >��Ńp���h�b�N�X���������̂̓J���g�[������Ȃ��������� >���b�Z���̃p���h�b�N�X��R={x| x��x}�Ɋւ���z �������܂��� �Ɗw���Ƃ��������Ƃ��낪����o���ɂȂ����Ⴄ >�^�͉����l�̉E���ɒ��߂Ƃ��ĕt���Ă銴���̃C���[�W >123 : ���R�� >�݂����� >����"���R��"���^ �m���ɂ��������g�������Ă�� �u�����͂���̌^�̗�ł��葼�̌^�̗�ł͂Ȃ��v �u���̌^�Ƃ͂��ꂱ��̏��������W���ł��� �i�����̂Ȃ��P�Ȃ郉�x���̓\��t����ꂽ�W���̂��Ƃ�����j�v �������H |
| �cNo.115427+�w���_�̕������x�Ƃ������ȏ��Ƃ���������w�u�`�̃J�^���O�݂����Ȗ{���邯�� ��4�́w�v���O�����Ӗ��_�ƌ��_�x�̗v��@������ �uCurry-Howard�Ή��Ƃ�����Ō^�͖���̂悤�Ȃ��̂ƌ��Ȃ���v�Ƃ����L�q�������� �ʂ̃v���O�����n�̐l�̏��������O�̒ʂ�w�^���_�x���Ė{���� �ϐ���ϐ��́i�����_�v�Z�́j���Ƃ��Ắu���v�́u�^�v���u�����v ���ۂɂ͌^�Ƃ͂܂��ʂ̕ϐ���ϐ��̉E�����ŏo���Ă��� �i�Ⴆ�ΐ����^���l�^���l�^��u�����^�i�̍��j����͂������l�^���l�^�i�̍��j���o�͂���Ȃ^�v���j �Ƃ������ƂŏW���Ƃ������͎��ƊW�̂��閽��Ƃ��čl�������������̂������� �ǂ������W���͂�����ƕ�����Ȃ��i�����W���Ƃ͍l���ɂ������珇�����Ή����Ǝv���j |
| �cNo.115428+������>>18�̓i�V �����Ƃ��ĉ��������߂�Ȃ��� |
| �cNo.115429+Curry-Howard�Ή����Ă̂͗Ⴆ�Ό^�t���v�Z�� �ux : double, f : double -> int �ƌ����f�[�^���� f(x) : int ���v�Z����v���O���������܂��v �ƌ��������̌^�̕������������, �udouble, double -> int ���� int ���v�Z�ł��܂��v �ƂȂ���, ���ꂪ�_���w�� �uA, A -> B �����肷��� B ���������v �i���[�_�X�E�|�l���X�j �ƂȂ��Ă�˂��ĂȂ�z���� ���������ۓI�ȊW������^�i�����Ō���double, int�j�Ɩ���iA, B�j�������ł�����Č����Ă��u�H�v���ĂȂ邾���ȋC������ �W��{1,2,3}��{���,�݂���,�o�i�i}�����^�ł�����Č����Ă�1=���,3=�o�i�i�������I�Ƃ͂Ȃ�Ȃ��̂Ɠ��������� |
| �cNo.115430+�����W���ɂ͌��\���Ă�C������, �Ⴆ�� x : double, f: double -> int ���Ă����̂�, x �� double, f �� Map(double, int) �iMap(A,B)�͏W��A����W��B�ւ̊��̏W���j �ƌ��������Ĉ�a���Ȃ��� |
| �cNo.115431+����͐^�U�l���t���Ȃ��Ⴂ���Ȃ��Ƃ�������t�������nj^�ƏW���͂��������̂Ȃ��̂��傫�ȈႢ�� |
�cNo.115450+  �Ȃقړ����݂����Ȃ̌����� �^�����Ȃ̂��͐F�X���߂̗]�n������炵���ƌ������^���Ă��ꂾ���F�X�Ȃ��̂ɋ��ʂ��������i�`���H�j���������Ă��Ƃ�>��F�u�^�̗��_����v>�y�[�W 169https://www.marulabo.net/docs/type-theory-2/ |
�cNo.115451+  >�Ȃقړ����݂����Ȃ̌����� ���`���N�`���A�c�C�Ȃ���Ƃ��̑O�̃v���[�������^�Ƃ͑f�p�ɂ͂܂��u�v�f��ʑ��ɔ����Ă��鉽�炩�̐����̏W���v������������́u�K�w�\���������Ă��莩���̌^�̉��ʂłȂ��^�ɂ͎ʑ����g�������ւ����Ă�����́v�ł��������̔���́u�����v�f���ؖ��Ɍ����ĂČ^�𖽑�Ɍ����Ă��猋�_�ƂȂ閽�肪�W�Ȃ����̓��m�̏ؖ����m���֘A�t���Ă����̊֘A�t�����ʑ��͂ǂ����̌��_�ɂ��s������Ȃ����狏�ꏊ�Ȃ������v�Ƃ����邢�́u�����v�f��_�Ɍ����ĂČ^����ԂɌ����Ă����Ԃ��W�Ȃ����̓��m�̓_���m�̊Ԃ̐����ǂ������̋�Ԃɓ����Ă��Ȃ������v�Ƃ������I�ɂ͂��������Ӗ������ɂȂ�̂��Ɖ��߂����悽�Ԃ̉摜�̂悤�Ȋ����ł͂Ȃ��낤���i�����ˁ[�菑���Ő\����Ȃ����j |
| �cNo.115452+���[������ ���[�_�X�|�l���X�Ɗ��K�p�����̎��Ă邩�H���Ęb�̗����������Ȃ��Ă���Ęb���ȁH����Ƃ� >No.115424 �̏W���A�W���̏W���A�W���̏W���̏W���A�c���ĊK�w���^�ɂ͔�����Ă���Ęb�̕����H |
| �cNo.115453+>���[�_�X�|�l���X�Ɗ��K�p�����̎��Ă邩�H���Ęb�̗����������Ȃ��Ă���Ęb���ȁH �������ɋ߂��b���� �u�v�fa���W��A�ɏ�������&�v�fb���W��B�ɏ�������Ƃ� �����̊Ԃ̎ʑ���A�ɂ�B�ɂ��������ĂȂ� ����͘_�����ł��_�ł������ł��� ���́u�Ⴄ�W�����m�̗v�f���m�̎ʑ��͂ǂ���̏W���ɂ��������Ă��Ȃ��v���Ƃ���������� �u�Ⴄ�^���m�̗v�f���m�̎ʑ��͂ǂ���̌^�ł������Ȃ��v�Ƃ������ƂƗv�͓����Ӗ��Ȃ̂� �܂��͂�^�Ƃ͏W���̂��ƂȂ̂ł́H�v�Ƃ������Ƃ����������}������ |
| �cNo.115454+>�W���A�W���̏W���A�W���̏W���̏W���A�c���ĊK�w���^�ɂ͔�����Ă���Ęb�̕����H �������͂������̐}�ł͕`���Ȃ������� �^A�̕����W���Ƃ��ĉ��ʊK�w�̌^S���l���� S�̒��̗v�fa'��z�肵���瓖�R����͌^A�̗v�f�ł�����̂� a��a'�̎ʑ��͌^A�̒��Ŗ��Ȃ������邵�O�q�̒ʂ�^A�̊O�ɂ܂����ƈ����Ȃ��Ȃ� ����Ȃ��͂肳�����������ʂ�u�^=�W���v�Ƃ����F���ł悳���� �i�W���̏W���]�X������u�傫���Ȃ�v�Ǝv������ �����W���]�X�́u�������Ȃ�v�b�ɂȂ��Ă���͎̂����ł����������邪�j |
| �cNo.115455+�K�w��������Ęb��x��x�݂����Ȃ̂�����邽�߂� (x : A) �� (y : B), (B��A����ʂ̌^) �݂����Ȋ����ŗ��ӈႤ�^�ɂ��悤���Ă����b�������Ǝv�� �����W���Ƃ͂܂�������ƈႤ�C������ |
| �cNo.115457+https://proc-cpuinfo.fixstars.com/2017/05/division-operation-optimization/ �O���^���f�B�[�N�\�� �� ���̐��̕␔�\�� �� �f�B���b�N�̊C |
| �cNo.115458+�O���^���f�B�[�N�\�����ėv�f�̌��̈�ʓI�ȓz�炵�����nj^�Ɖ����W����́H |
| �cNo.115470+�T������j |
| �cNo.115471+�Â߂��������P�������ō��ؒ��J�Ș_���w�̋��ȏ��ł��� �O������w�L���_������x�̑�8�́�1��ǂ�ł����� >��F�Ƃ���F�̂悤��<�q��Ɋւ�������p�f>�������킹�l����_����2�K�̏q��_���Ƃ����܂��B ><�q��̏q��>�Ɋւ�������p�f������3�K�̏q��_���Ƃ����悤�ɁA���K�̏q��_��-���邢�͌^�̗��_�Ƃ�����-�Ƃ������̂���ʂɍl���邱�Ƃ��ł��܂��B ���Ă������̂� ���̖{�̑�1�ł�1967�N10��15���Ȃ�� �����u���K�̏q��_�����^���_�v�Ƃ����F�����������Ƃ������Ƃ��ǂݎ��� �܂����̖{�ł͑�1�́�5�ŏq��Ɛ����ƊT�O�Ə����Ɩ�����Ɓi����ŏ�����j�W���ꎋ����̂� �܂�͌^���q��̏q�ꁁ�i����ŏ�����j�W���̂���Ȃ�i����ŏ�����j�W���ł���ƍl������ ���ꂾ�ƍ��܂ł̋c�_�Ɛ����I�Ȍ����ł����� |
| �cNo.115476+���j�I�ɂ̓��b�Z�����W���_�̃p���h�N�X��������邽�߂ɓ��������̂��^(�^�C�v)�����ǁA���b�Z��(�ƃz���C�g�w�b�h)�͂���ɈӖ��_�I�p���h�N�X�Ƃ����̂�������邽�߂ɊK(�I�[�_�[)�Ƃ����̂����������B �ł������͒�`�ɂ���Ă͓����ɂȂ�̂őO���搶�Ȃ͓��ꎋ���ċ��ȏ������������B ����ƌ^�ꎋ����̂́A���R��㈂̏ؖ��ƌ^�t���̓��o�̌n�����^�ɂȂ邩��Ƃ��������łȂ��A����̈Ӗ������̏ؖ��̏W�܂�Ɠ��ꎋ����(BHK����)�ƌ^���ۂ��Ȃ�Ƃ����w�i������B �v���O�����̕\���I�Ӗ��_�Ƃ����̂�^����ƃv���O�����̌^�𐔊w�I�ȏW���ƑΉ��Â�����悤�ɂȂ��B |
| �cNo.115757+>���j�I�ɂ̓��b�Z�����W���_�̃p���h�N�X��������邽�߂ɓ��������̂��^(�^�C�v)�����ǁA���b�Z��(�ƃz���C�g�w�b�h)�͂���ɈӖ��_�I�p���h�N�X�Ƃ����̂�������邽�߂ɊK(�I�[�_�[)�Ƃ����̂����������B >�ł������͒�`�ɂ���Ă͓����ɂȂ�̂őO���搶�Ȃ͓��ꎋ���ċ��ȏ������������B ���C�Â������Ǖʕ��Ȃ�ł����I�@�������Ă��c |
| �cNo.116049��������x1PM�i�v�����L�s�A�E�}�e�}�e�B�J�j�ł͏�ł����Ă�悤�ɕʊT�O�Ƃ��Č^�ƊK���������ǁC������̃Q�[�f����ɂ���Ă��ȕւɍĒ�`�����D������͌^�ƊK��������ʂ��Ȃ��Ă����D �ꉞ�C�Q�[�f���̒�`�ł��K�͘_�����̊K�w�̂悤�ȊT�O�Ȃ̂Ō^�Ƃ͈Ⴄ����ǁC��������Ɠ��l�̌����ɂ���ďW���̈��ł���^�Ƙ_�����̐����ł���K��Ή��t���Ă���D >�^���ĂȂɁH �قڏW���_�Ō����Ƃ���̃N���X�i�ށj�Ɠ����D �ł����b�Z���̃p���h�N�X�̂悤�Ȃ��̂@�I�ɔr�����邽�߂ɁC�Ώۂ̋A���W�̊K�w�i�����j�̂悤�Ȃ��̂�t�^���āC�ЂƂ�̊K�w����̋A���ɂ������@�I�Ɍ��y�ł��Ȃ��悤�ɐ����������_��������D ���������\���t���N���X�̂��Ƃ��C���邢�͂��̃N���X�Ɋ���U��ꂽ�K�w���������郉�x���̂��Ƃ��^�Ƃ�D �K�̓Q�[�f���I�Ȍ^�ɑΉ�������`�Ȃ̂��C�ʉ��̋����Œ�`����̂��Ȃǂł���������Ⴄ���Corder��sorted�̗p�ꂪ���j�I�Ƀ��[�Y�Ɏg���Ă���D ����ɂ��ẮC2�K�q��_���̕W�����߂Ɣ�W�����߂₱��ɔ����w���L���̎d���ɁC���̂�����̃��������𐰂炷����������D |