
Name名無し21/02/24(水)12:28:58No.114887+
22年1月頃消えます 宇宙空間に N 個の惑星があります。それぞれの惑星は球で、すべて同じ半径です。(仮に半径Rとします)
惑星の表面のうち、他の惑星の表面からは見えない土地を隠れた土地と呼ぶことにします。
すべての惑星の隠れた土地の面積を合計するといくつになるでしょうか。 削除された記事が8件あります.見る
| …No.114888+そもそも宇宙の形はどうなってるんだ? |
| …No.114889+書き込みをした人によって削除されました |
| …No.114890+> そもそも宇宙の形はどうなってるんだ? 書き忘れていましたが普通の3次元ユークリッド空間です。 |
| …No.114891+惑星の表面からは見えない土地を問う問題なのに 惑星の表面から立ち上がった人っぽいブツが 他の惑星を見ているスレ画は不適切 |
| …No.114892+書き込みをした人によって削除されました |
| …No.114893+勘で(4πR^3)/3 くらい |
| …No.114894+惑星直列だった場合は自明に球1個分の表面積になり、他の配置でもNによらず同じになるんだろうなと予想は立つ |
| …No.114896+N個の惑星の隠れた土地を平行移動すれば 惑星の配置によらず半径Rの球面にできるので4πR^2 |
| …No.114897+書き込みをした人によって削除されました |
| …No.114898+平行移動したら星がぶつかったりすり抜けたりする場合は一体…… |
| …No.114899+書き込みをした人によって削除されました |
| …No.114900+一般的に星は自転するのでそれを考慮するべきなんだろな |
| …No.114901+書き込みをした人によって削除されました |
| …No.114902+書き込みをした人によって削除されました |
| …No.114903そうだねx1平面上に3つの惑星A、B、Cを中心が正三角形の頂点をなすように配置汁、 この状態ではA、B、Cの隠れた土地を平行移動して貼り合わせて半径Rの1個の球にでき、 その合計面積は4πr^2 (= 1惑星表面積)である (惑星1個あたりの隠れた土地の面積は1/3惑星表面積となりぬ、 ここでさらに惑星Dを、次の条件を満たす位置に配置する。 (1) ∠BDC = 90° (2) Aから△BDCに下ろした垂線の足がDに一致する このときDの隠れた土地は、Dの全表面がB、Cによって1/4となり、 Aによってそれがさらに半分となるから1/8惑星表面積、と結論さるる、 一方、A、B、Cの3惑星系において隠れた土地だった1惑星表面積のうち、 Dから見えてしまう(隠れた土地でなくなってしまう)面積の合計は、 B、Cの合計だけでも明らかに1/3惑星表面積の半分(=1/6)は超えるから、 1/8惑星表面積より大きいつまりDの導入によって隠れた土地は1惑星表面積未満となる |
| …No.114904+と思ったが B、Cの合計だけでも明らかに1/3惑星表面積の半分を超えるかはビミョーか、orz |
| …No.114905+書き込みをした人によって削除されました |
| …No.114907+ちゅかもっとわかりやすい例を思いついたわ;; A B C D F という星の配置があり、C、D、Fは一直線上にならんで「いない」とする。 これにABの中間あたりにA、E、Bが一直線となるように星Eを加えてみる: A E B C D F EはABに挟まれているから、隠れた土地を持たない。つまり隠れた土地は増えない。 一方、Eの地表から見える分CやDやFの隠れた土地は、 Eの地表という新たな視点から見られることで減ることが有り得る。 よって、Eを加える前も加えた後も常に4πR^2で一定とは限らず、面積が減るケースが存在する。 |
…No.114908そうだねx3 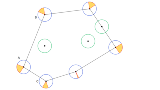 全惑星の中心が同一平面上にある場合、隠れた土地の合計が4πR^2になることの証明 N個の星のうち何個かの中心を結び、N個全ての星がその周上or内部に含まれるような凸多角形Xを考えることができる。(N個が同一直線上であれば両端の星の裏表で星1個分の表面積になることは明らか)このとき、Xの頂点を構成しない星(緑色)に隠れた土地は存在しない。Xの頂点を構成する星(青色)について、図の星Aで考える。Xの前提条件より∠BACの内側に全ての星が含まれるのでAの隠れた土地は黄色の扇形であり、その中心角は頂点AでのXの外角の大きさに等しい。(図は目分量で描いたので正確ではない)したがって全頂点について扇形の中心角を足し合わせるとXの外角の和360°に等しくなり、隠れた土地の面積の合計は星の表面積1個分の4πR^2になる。これを3次元空間に拡張して凸多面体で考えれば同じような証明を作れそうだがそこまでの技量はなかった |
| …No.114909そうだねx1No.114907は撤回、惑星Eを追加しても別に新たな隠れた土地は生じなかた、、orz 惑星の矩形配置、正四面体配置、正四面体配置を貼り合わせた配置でも 隠れた土地が1惑星表面積になるのは自明なので、もっと歪んだ立体を考える、 いま惑星A、B、Cが正三角形状に配置しているところに惑星Pを追加して、 ∠PAB = ∠PAC = 90°、∠PBA = ∠PCA = 45° と汁、するとその他の角は∠PBC = ∠PCB = 69.30°、∠BPC = 41.41°となりぬ、 で、星Xから星Yを見込んだ時星Y地表には隠れた土地とそうでない土地の境界が 大円となって現れる。上記の角度はこの大円の交差角度に外ならず、 隠れた土地は交差角のうちの鈍角を頂角とする球面三角形であるから、面積は以下の通り: A: 頂角120°、90°、90°の球面三角形、面積=2/3πR^2 = 1/6惑星表面積 B: 頂角120°、135°、110.7°の球面三角、面積=1.032πR^2 = 0.258惑星表面積 C: 頂角120°、135°、110.7°の球面三角、面積=0.258惑星表面積 P: 頂角135°、135°、138.6°の球面三角、面積=1.270πR^2 = 0.317惑星表面積 合計すると0.9996惑星表面積、、orz |
| …No.114910+なぜじゃ!納得いかねーヽ(`Д´#)ノ ムキー!! |
| …No.114918+宇宙の真理はもっと簡単なはずだ |
| …No.114919+>No.114918は無理数を見て人を頃すタイプ |
| …No.114925+>無理数を見て人を頃すタイプ ピタゴラス学派かクロネッカーかな? |
| …No.114926+クロネッカーは整数以外は人が作った数だと言いはしたが 別にカントールに直接手を下して海に突き落としたわけではないし、 ていうかピタゴラス学派は論文非公開でどうやって生計を立てていた んですかね…… |
| …No.114932+>クロネッカーは整数以外は人が作った数だと言いはしたが >別にカントールに直接手を下して海に突き落としたわけではないし、 >ていうかピタゴラス学派は論文非公開でどうやって生計を立てていた >んですかね…… ボルツマンとかカントールってかわいそうだよねー |
| …No.114938+書き込みをした人によって削除されました |
…No.114948そうだねx1 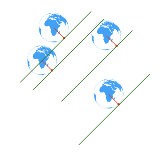 全ての星の表面について共通の座標(経度λ,緯度φ)を設定したとき、 星kの表面上の点A_k(λ,φ)が隠された土地になる条件は、n個全ての星が、球面kの点A_kでの接平面に対して片側だけに収まることである。(そうでなければ、接平面のもう片側にある土地から見られてしまう)言い換えると、星の中心から点(λ,φ)へと向かった方向を向いた時、n個の点(λ,φ)の中でが最も向こう側にある点が隠された土地となる。したがって、任意の座標(λ,φ)に対して1個の星に対応するものだけ[※]が隠された土地になる。(図で言えば右下の星の点、図は上のURLから引用)以上より、隠された土地の面積の合計は1個分の星の表面積に等しい。[※]隠された土地となる点の接平面が複数の星に接する場合もあるが、 そのような点は幅を持たないので面積計算上は無視できる。 |
| …No.114971+(λ,φ)と隠れた土地の接平面と惑星表面の交点が 必ず1対1対応だから(λ,φ)の全値域について交点 の面積を積分したら1惑星分とか 公理から出発して形式的に書き表すにはどうすればいいんじゃ…… |