Name名無し21/05/18(火)00:15:08No.115212+
22年4月頃消えます プログラミング初心者の本を読んでるとジャンケンをするプログラムが載ってるんですが
グー＝0
チョキ＝1
パー＝2
としてコンピュータとじゃんけんをして
引き分け＝0
勝ち＝1
負け＝2
という答えを導き出すにはどうすればいいでしょうか。
本に式とプログラムは載ってるんですが説明が無いので理解できないのです。
当方の数学の知能は小学生レベルです。 削除された記事が4件あります.見る

…No.115213+書き込みをした人によって削除されました

…No.115214+書き込みをした人によって削除されました

…No.115215+ 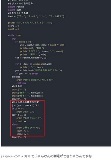ネットに同じのがありました。 赤で囲んだ部分です。（pythonで％は「割った余り」という意味です）なぜ自分の手から相手の手を引いて3を足して、3で割った余りが、勝敗の値になるのでしょうか。どうやってその式を導き出したのかがわからないです。

…No.115216+ 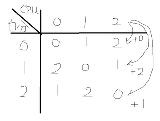以下全部mod 3で考えるとする.(要は1+2=0, 2+2=1などなど…) 自分の手とCPUの手,そのときの勝敗を表にまとめると図みたいな感じになる自分の手=i, CPUの手=jとしてやると,勝敗(i,j)| i == 0 -> j| i == 1 -> j + 2| i == 2 -> j + 1となってる事がわかる. mod 3に注意すると,勝敗(i,j)| i == 0 -> j + (3 - i)| i == 1 -> j + (3 - i)| i == 2 -> j + (3 - i)となる. 全部同じ形に変形できたから,勝敗(i,j) = j + (3 - i)自分の手と勝敗の和が常に0になるのを表から読み取れたら早いけど、気づかなかったらこんな感じ地道にやるとわかる

…No.115217+f(x) | x == a -> a' | x == b -> b' ... は x == a のとき, f(x) の値は a', x == b のとき, f(x) の値は b', ... と読んで

…No.115218+ちなみに >ネットに同じのがありました。 と言ってるけど >1621265213784.jpg は 引き分け＝0 勝ち＝2 負け＝1 になってるから注意

…No.115219+誤）自分の手と勝敗の和が常に0になる 正）自分の手-相手の手と勝敗の和が常に0になる

…No.115220そうだねx1スレ主ですが、その図まではわかるんですが、 当方小学生並みの算数しか知らないので MOD3とか==とか->の意味がさっぱり分からないです

…No.115221+mod 3 で考えるっていうのは数字を3で割った余りが同じなら同じとみなしますよということ つまり, ...=-6=-3=0=3=6= 9=12=..., ...=-5=-2=1=4=7=10=13=..., ...=-4=-1=2=5=8=11=14=... こうすることでこの世の数（整数）は0,1,2のどれかになる 例えば100だったら,100÷3=33あまり1だから1と同じ >1621283363692.png には0,1,2しか出てきてないからmod 3で考えると都合が良さそうだなと言う発想になるわけ ==は大抵のプログラミング言語で等しいことを表す記号 普通の=一個だと代入記号とややこしいから便宜上そうなってる ->はオリジナルの記号で意味は>No.115217 に書いた通り

…No.115222+補足するとデジタル時計の時間表記はmod 24だね 0時, 1時, ..., 23時ときてその次は24時じゃなくて0時に戻る 24を24で割った余り = 0を24で割った余り = 0 つまりmod 24の世界では24と0は同じ数 同様に25時は1時のことだよね なぜなら, 25を24で割った余り = 1を24で割った余り = 1 つまりmod 24の世界では25と1は同じ数 普通のプログラミング言語ではaをbで割った余りのことを a % b と書く. pythonでもそう この表記で行くと, 22時の10時間後は32時と言ってもいいけど普通は 32 % 24 == 8 だから8時ということになる

…No.115223+北風と太陽の童話を思い浮かべたら良い グー → チョキ → パー → グー → チョキ→ パー …… の順にグー、チョキ、パーさんが家を構えて住んでいたとする いま一番左のグー氏の住所を0としたら、グー氏は 1軒右（住所1）の住人（チョキ）には勝って、2軒右（住所2）の住人（パー）には負ける 住所1の住人チョキ氏は 1軒右（住所2）の住人（パー）には勝って、2軒右（住所3）の住人（グー）には負ける 住所2の住人パー氏は 1軒右（住所3）の住人（グー）には勝って、2軒右（住所4）の住人（チョキ）には負ける という関係にある

…No.115224+書き込みをした人によって削除されました

…No.115225+さらに、3軒右まで進むと、誰さんも同じ一族の家に行きつく （グーならグー、チョキならチョキ、パーならパーの家に着く）から勝ちも負けもなくあいこや ここまでの話では、左方向に何軒離れているかでは勝ち負けがさっぱりわからないから、 とにかく　①相手より右隣にある　②同族の家　に出撃してもらう方針に汁、 当方がグー（住所0）なら、チョキ（住所1）やパー（住所2）の右隣であるグーの一族は住所3や 当方がチョキ（住所1）なら、グー（住所0）やパー（住所2）の右隣であるチョキの一族は住所4や 当方がパー（住所2）なら、グー（住所0）やチョキ（住所1）の右隣であるパーの一族は住所5や 何にせよ3を足したら出撃いただくべき家の住所がﾜｶﾙ で、（出撃いただく家の住所）-（相手の手の住所）が1なら、相手のすぐ右隣なので当方の一族が負ける 　　（出撃いただく家の住所）-（相手の手の住所）が2なら、相手の2軒右隣なので当方の一族が勝つる 　　（出撃いただく家の住所）-（相手の手の住所）が3なら、同族なのであいこや

…No.115226+書き込みをした人によって削除されました

…No.115227+いやちょっと待てや、 とここで同族からクレームがつくことがある 1) 当方がチョキ（住所1）で相手がグー（住所0）のとき 2) 当方がパー（住所2）で相手がグー（住所0）のとき 3) 当方がパー（住所2）で相手がチョキ（住所1）のとき これらのいずれかのとき、 （出撃いただく家の住所）-（相手の手の住所）で計算した出撃いただく家が 相手から4軒以上右に離れてしまう。このときは3件戻した家を戦いの当番にせねばならない（それが相手に最も近い右隣の家にあたる そうするには%3を使い、 　1)のとき: （（出撃いただく家の住所）-（相手の手の住所）) % 3 = ((1+3) - 0) % 3 = 1 　2)のとき: （ (出撃いただく家の住所) - (相手の手の住所) ) % 3 = ((2+3) - 0) % 3 = 2 　3)のとき: （ (出撃いただく家の住所) - (相手の手の住所) ) % 3 = ((2+3) - 1) % 3 = 1 と計算しておけば、常に相手から3軒以内で出撃すべき家が決まって丸く収まる

…No.115228そうだねx1> グー＝0 チョキ＝1 パー＝2 としてコンピュータとじゃんけんをして > 引き分け＝0 勝ち＝1 負け＝2 という答えを導き出すにはどうすればいいでしょうか。 答え = (自分の手 + 自分の手 + 相手の手) % 3 でもいいかも

…No.115229+ これは初心者には無理

…No.115236+ジャンケンマンのアルゴリズムってどうなっていたんだろ？ あちこちに置かれていて、異彩を放っていたよな。 こっちがランダム戦略を取れば一定の確率で勝てる場合もあるのか？

…No.115237+あーいこーでしょ！でしょ！でしょ！やったー

…No.115239+> こっちがランダム戦略を取れば一定の確率で勝てる場合もあるのか？ グーチョキパーを1/3の確率でランダムに出せば勝ち、負け、あいこが1/3ずつになるはず もし結果が1/3ずつにならなければ何かズルをしている(後出しとか)