Name名無し21/01/10(日)11:31:02No.114764+
21年11月頃消えます この問題。無限の計算時間と無限の記憶域があれば高卒の俺でも解を求められるけど東大生が5秒くらいで解くのを見ると地頭の違いを見せつけられる。
今の脳みそに未練はないから早く半導体と統合したい。 削除された記事が1件あります.見る

…No.114765そうだねx1高さが1増えるごとに5列ずつ増えてるのが分かれば7段あるから 5*(1+2+...+7)=5*7*8/2=140個 規則的に並べられてるからパパっと答えが出せる

…No.114766+地頭というかクイズに対する知識だな

…No.114767+頭の良さというより経験だね

…No.114768+>高さが1増えるごとに5列ずつ増えてるのが分かれば7段あるから なるほど、そのアルゴリズムを用いると効率的に解が求まることが高卒脳でも理解できた。 さらに「ブロックの段数」「最上段と最上段-1のブロックの数の差」の情報があれば答えが出る問題なんだろうなと予想できた。 でも俺が「ブロックの段数」を数えている間に東大生は答えを出しているから空間認識能力から違うんだろうなと思った。

…No.114769+>でも俺が「ブロックの段数」を数えている間に東大生は答えを出しているから空間認識能力から違うんだろうなと思った。 その番組見てないから分からんけど多分数えながら回答ボタン押してるんだと思う 大抵の早押しクイズは問題が表示されてから実際に回答するまでに結構ラグがあるからな

…No.114770+ 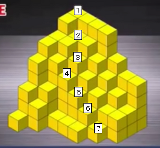こうやって数えれば短時間でブロックの段数が解った。 ブロックの段数は７ブロックの最上段と最上段−１の差は５という情報を短時間で得る事が出来たけど高卒で離散数学のセンスが無いから計算に30秒はかかってしまう脳に直接半導体を搭載してクロックアップ図らないと5秒程度じゃ答え出せないだろうな技術の発展が待ち遠しい

…No.114771+>大抵の早押しクイズは問題が表示されてから実際に回答するまでに結構ラグがあるからな 件の問題探してたら下のを見つけた。 https://www.youtube.com/watch?v=bzpTOjQkTKk 立方体の面積という、さらに計算能力を求められる問いを3秒くらいで解いてた。 もう俺の高卒脳みそは半導体と融合じゃなくて半導体に全取り換えで良いです。己の脳への依存を止め計算機工学の進歩に依存します。

…No.114772+クイズに強い人はシンキングタイム中に答えを導くまでの時間を逆算して早押しするスキルを持っている

…No.114773+ これを３秒とか東大医学部の脳はどうなってるのか。。。

…No.114774+フラッシュ暗算の方がどうかしていると思う

…No.114788+>でも俺が「ブロックの段数」を数えている間に東大生は答えを出しているから空間認識能力から違うんだろうなと思った。 その東大生が、アルゴリズム(？)を明確に認識する過程で段数も数えている ということは大いに考えられる >その番組見てないから分からんけど多分数えながら回答ボタン押してるんだと思う それもあり得る

…No.114789+>フラッシュ暗算の方がどうかしていると思う フラッシュ暗算は単純作業だよ 慣れれば速くなるのは想像がつくよ

…No.114799+>>フラッシュ暗算の方がどうかしていると思う >フラッシュ暗算は単純作業だよ >慣れれば速くなるのは想像がつくよ ずっと指折りながら数えててもいつまでも遅いままでしょ 要はやり方と子供の頃の教育が重要

…No.114800+ No.114770 下のクイズ動画だと『９個ずつ増えてる』と法則を述べてるこの画像だと1から100までの数の和の ガウスの例を利用すれば一番下は 7ｘ5＝35 +５で 和は4035＋５＝40 よって （４０ｘ７）/２＝１４０謎解きは楽だが一瞬で法則性を理解して 置き換えるのは難しいね

…No.114801+クイズが等差数列の問題だと理解できたら 速いんだろうな

…No.114802+【頭脳王】''積み重ねられたブロック''集 - YouTube https://www.youtube.com/watch?v=GlECAh1pa7c 頭脳王って番組で 2011年から 類型の問題になってる、 過去問を知ってるかどうかだと思う

…No.114803+書き込みをした人によって削除されました

…No.114804+ https://www.youtube.com/watch?v=bzpTOjQkTKk この画像の場合は 毎年出てる 立方体カウント問題の応用編一番上のキューブは９個以下 次段以降 ９個づつの構成 段は １０段毎年出てるので ひっかけ問題ではないと仮定して１０段目(底のキューブは)９０個{（９０＋９）* １０段}/2＝９９０/2＝４９５立方体 １個は ８cm３なので４９５ｘ８を計算してもいいが インド式に計算して９９０ｘ４＝３９６０＝ (1000ｘ4)-(10ｘ4)＝３９６０

…No.114807+頭脳王 種明かし 立方体の数を求める（頭脳王） - ありかぶろぐ https://sites.google.com/site/hakase0617arika/jiaoerutoiukoto/li-fang-tino-shuwo-qiumeru-tou-nao-wang

…No.114808+この立方体問題 毎年ほぼ同じ問題が出題だってさ 暗記ゲーやな 2018年は7×55×8=3080立方センチメートル 2019年は8×55×8=3520立方センチメートル 2020年は9×55×8=3960立方センチメートル が答えとなっているので、 2021年に 出題されるとしたら 10×55×8=4400立方センチメートル が正解となる可能性が高いでしょうとの事

…No.114809+解法 段が１０段の場合は １〜１０を足した総和 ５５を覚えておく スレ画の場合は ７段なので １〜７の総和 (8*7)/2=28を暗記しておく 増える数 ５ｘ 段の総和 ＝全体の 立方体の総数 ５ｘ２８ ＝１４０が 答え 例年のパターンとして 『一番上のキューブの数＝増加する個数』毎回同じ あとは 総和のパターンを暗記しておく 個数問題が予選で出て 決勝問題では 個数ｘ８cmが毎回同じ出題 こんな感じらしい

…No.114810+>毎年ほぼ同じ問題が出題だってさ 暗記ゲーやな 雑学王なんかの番組でも雑学の本から出題するから、その雑学本をいくら暗記してるかを競うようなもんだよな 既に「雑学」ではない

…No.114850+>が答えとなっているので、 >2021年に 出題されるとしたら 作問側の怠慢と言われても仕方ないねこれは

…No.114965+これ計算というよりは典型問題ってことでいいのかな？

…No.114979+>>毎年ほぼ同じ問題が出題だってさ 暗記ゲーやな >雑学王なんかの番組でも雑学の本から出題するから、その雑学本をいくら暗記してるかを競うようなもんだよな >既に「雑学」ではない 体系立った知識を勉強する方がマシかな 雑多な個別の知識から体系を見出す方が研究や学問にはずっと迫ってるが

…No.114980+スレ画の問題文だけだと、死角の部分にブロックが積まれている可能性は排除できないんじゃないか？ 積まれている場所が平面だと示されてもいない

…No.115011+ 本文無し

…No.115012+上甲板の上だけで10段×24×24=5760個ぐらいありそう 半分の長さのコンテナはニコイチで数えるとして、

…No.115170+積み重ねられたブロックだから、一段のブロックは除いた方がいいのでは？と言ってみる

…No.115177+ブロックAの上にブロックBが乗っているとき、 積み重ねられているのはAとBのどっちなのや ろうか……

…No.115178+つかブロックがブロックを積み重ねるのではなく、 神がブロックを積み重ねるのだとしたら 積み重ねられるブロックはA、B両方該当するのではな いか、

…No.115184+塾かどこかで過去問解いてて 当てはめただけ？