 Name名無し20/08/12(水)08:06:49No.114409+
7月02日頃消えます
圏論の魅力
Name名無し20/08/12(水)08:06:49No.114409+
7月02日頃消えます
圏論の魅力
| …No.114410+自然変換が分からない |
| …No.114411+>自然変換が分からない 関手の間の射だよね F, G: C -> D を圏Cから圏Dへの関手としたら 実際はDの対象間の射の族(η_A:F(A)->G(A))_{A∈object(D)}で自然性公理を満たす奴 関手が既に矢印なのにその矢印から矢印への矢印が定義されるってことに衝撃を受けた記憶 |
| …No.114412+object(C)だったわ |
| …No.114415+>>自然変換が分からない >関手の間の射だよね >F, G: C -> D を圏Cから圏Dへの関手としたら >実際はDの対象間の射の族(η_A:F(A)->G(A))_{A∈object(D)}で自然性公理を満たす奴 >関手が既に矢印なのにその矢印から矢印への矢印が定義されるってことに衝撃を受けた記憶 「手段の目的化」を論じる数理的手法に使えないか一時期考えてたことがあるが なんも思い浮かばなあった |
| …No.114416+>「手段の目的化」を論じる数理的手法 気になる |
| …No.114417+マルコフ圏というのを考えると確率論が測度とかのごちゃごちゃした議論無しにスッっと定式化されるらしい |
| …No.114418+長年に渡って意味不明だったけどロボット工学の同次変換も圏論っぽいんじゃないかと考えたらちょっとお近づきになれた気がする |
| …No.114419+線形空間の圏の部分圏かな |
| …No.114420+>長年に渡って意味不明だったけどロボット工学の同次変換も圏論っぽいんじゃないかと考えたらちょっとお近づきになれた気がする ロボット工学はもっとふつうに解析力学→シンプレクティック幾何→圏論の抽象化方面だろ |
| …No.114429+情報分野で使われてるイメージ 対象は型で射はある型からある型へ関数って圏を考えたり 対象が関数の出力した値で射はその値の近似度って圏を考えたり |
…No.114433+  現代数学だと圏論というよりコホモロジー |
| …No.114467+普遍性って大事なの・・・? |
| …No.114468+圏論は全く知らないけどプログラミングのラムダ式は知ってる ラムダ式に例えて各概念を説明してほしい |
…No.114469+ 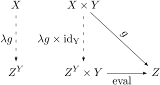 >圏論は全く知らないけどプログラミングのラムダ式は知ってる >ラムダ式に例えて各概念を説明してほしいλ式が関係ありそうな圏論の概念ってカリー化ぐらいな気がする集合で言えば(Z^Y)^XとZ^(X×Y)は同型って奴 |
…No.114471+ 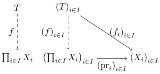 >普遍性って大事なの・・・? 直和とかテンソルとかいろんなものの定義の根底にあるのが普遍性だから大事は大事なんじゃないNo.114469のベキ対象も普遍性で定義されるし、直積も普遍性の図式で定義される |
…No.114476+  well-definedの定義も普遍性図式だから数学上の物を何か定義した時に自動的に普遍性を持つ事も多いのでは |
| …No.114477+イデアルで割った商集合、準同型定理が適用できる範疇が主題と言ってもいいぐらいだ |
| …No.114479+「モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも?」 とか一度は言ってみたい |
| …No.114481+こういう図式ってどれが与えられてるものでどれが「ただ一つ存在する」って奴なのかよくわからん |
| …No.114482+>こういう図式ってどれが与えられてるものでどれが「ただ一つ存在する」って奴なのかよくわからん 本文読むほかない気がする 図式からだけじゃわからないんじゃないかな 次の図式を可換にする射fが唯一存在するみたいな文言が本文にあるはず |
| …No.114519そうだねx1Haskellのモナドすきだよ |
…No.114821そうだねx1 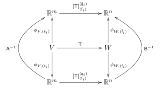 圏論ってわけじゃないけど線形代数の基底取り替え公式を可換図式にまとめるとすごくスッキリまとまる事がわかった https://amuthan.github.io/tensors-intro/linear_maps_1/ |
| …No.115059+いいですよね カリー=ハワード同型対応 |
| …No.115061+結局カリー=ハワード同型対応は何故成り立つんだろうか そもそも型とは一体何なんだろうか |
| …No.115094+Pを証明する図式とP->Qを証明する図式を組み合わせることでQを証明する図式を作ることが出来る それが関数呼び出しと同じだと気づくのがすごい |
| …No.115096+論理の 0->0 = 1 みたいなのは型の方だと ボトム型からボトム型への写像の型 = トップ型 に対応すると思うけどボトム型からボトム型への写像って何だ…?ってなる そしてそれが全ての型の親玉のトップ型になるとはどういうことなのか |
| …No.115098+あり得ないものを貰ったらあり得ないものを返すことができる という事なのかもしれない |
| …No.115099+ボトム型からボトム型への写像は空写像一つしかないからトップ型になるのは変じゃない? トップ型って要は全体集合みたいなもんじゃないの? 何か根本的な解釈違いをしてる気がする |
