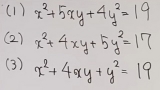
Name名無し20/10/21(水)00:59:29No.114537+
21年6月頃消えます 整数解を求めよ 削除された記事が1件あります.見る

…No.114538+だが断る！

…No.114539+書き込みをした人によって削除されました

…No.114540+25,-6 2,1 なし

…No.114541そうだねx1(1)(x+y)(x+4y)=19 (x+y,x+4y)=±(1,19),±(19,1) (x.y)=±(-5,6),±(25,-6) (2)(x+2y)^2+y^2=17 (x+2y,y)=(±1,±4),(±4,±1) (x,y)=±(7.-4),±(9.-4),±(2.1),±(6.-1) (3)左辺≡x^2+y^2≡19≡3(mod 4) nが整数ならn^2≡0or1(mod 4)なので上記を満たす整数x,yは存在しない

…No.114542+今見返したら,が.になってるとこあるけどまあいいや

…No.114549+https://www.youtube.com/watch?v=us-NAOQLYyA これの転載か

…No.114550+１番めと２番めの考えは分かる。 因数分解と x^2+y^2 の形にして場合分けってのは理屈にあっている。 でも３番めの mod4 を考える発想ってのはどこから来るのかｗ

…No.114551+こういうのって ディオファントス方程式？ になるの？

…No.114552+平方数（２乗の数）はmod3,mod4では0か1 にしかならないから