
| …No.114272+何か反例がありそう 双曲線と円弧を組みあわせるとか |
| …No.114275+>No.114272 円弧の方に2点ずつ取れば長方形できそうじゃない? 双曲線の方でもいいけど |
| …No.114276+書き込みをした人によって削除されました |
| …No.114277+書き込みをした人によって削除されました |
| …No.114278+三日月型は? 斜めに引き伸ばして左右反転の対称性をちょっと崩せば、 周上にとった2点を結ぶ線分の両端から 反対側の周に向かって下ろした足と周の交点2点を結ぶ線分が ぜってー平行にならないようにできそう |
…No.114302+ 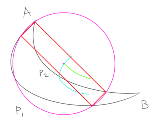 検証不足な主張が含まれているので証明とはいかないけど考察してみた 点A,Bとこの2点を繋ぐ互いに交わらない経路p1,p2があるこの経路上を互いの距離を一定に維持したまま動く点P,Qを考え,PQの中点が取る軌跡を考える点Aを出発する点をP,点Bを目指す点をQとする点Pが経路p1,点Qが経路p2を通る場合の軌跡(緑)と点Pが経路p2,点Qが経路p1を通る場合の軌跡(桃)について,これらが途切れずに引ききることが可能ならばこの2本は共有点を持つこの共有点を中心としPQを直径とする円 と 経路p1,p2 が交わる点を頂点に選ぶと長方形を作ることができる緑,桃が途切れる場合はPQの距離を変えるか点A,Bの位置を選び直すことによって条件にそぐう問題に帰着することができる |
| …No.114304+>No.114302 何となくわかる気がする。 ただ緑と青?(桃)の軌跡がどんな感じで動いたのか若干理解できなかった。 あとPとQは経路上の距離じゃなくて平面上の距離であってる? |
…No.114311+ 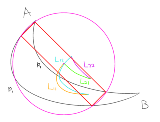 >No.114304 あってる点Pが経路p1,点Qが経路p2を通る場合の軌跡(L12,水)と点Pが経路p2,点Qが経路p1を通る場合の軌跡(L21,緑)の他に点P,点Qが経路p1を通る場合の軌跡(L11,橙)と点P,点Qが経路p2を通る場合の軌跡(L22,紫)を追加するとイメージがつかみやすいかも>No.114302は軌跡の色を途中で変更した際に文面上での更新を忘れた惑わせてすまない |
| …No.114313+>No.114311 なるほど じゃあ後はこれの正統性を示せればええわけや。 図形に対して二つの経路は取れると思うから、なぜ図形と円が交わるような中心ができるのかと、その円との交点で必ず長方形になることさえ言えればええんやな |