2月14日頃消えます 超天才

…

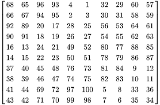
魔方陣？

…	魔法陣が可能な一辺のマス数って 無限にあるのかな？ 天才なら、証明できるもんかね？ もしそんな問題が、過去、論じられたことがなかったのなら 双葉数学の問題として、数学史の一ページに是非

…	奇数の魔法陣は中学で習うヒンズーの連続方式で簡単に作れる (4の倍数)x(4の倍数)の魔方陣も何かしらの法則に基づいて作れる 同様に(4n+2)×(4n+2) の魔方陣も手書きで作れる 斜めも含めた完全方陣は一辺nが4以上でかつ n≠4k+2 の時作れる 魔法陣の中に更に魔法陣が成立するものを親子魔法陣 すべての数を2乗しても、縦横の和が同じになる物を多重魔方陣 和がすべて異なるものをヘテロ陣 その和がすべて連続数になっているものをアンチ陣 2x2はもちろん、偶数x偶数の魔法陣は作れないものもある

…	すげー お詳しいのですね

…	素数だけで魔法陣って作れるの❓

…	素数は無限に存在するので 3x3の魔法陣は無限の組み合わせがあるとされてます 更には、連続した素数であっても4x4〜9x9までは既に見つかってます ちなみに、素数3から、nxnの数だけ足していった合計をnで割ると、縦横の和の最低数が出るので 少なくともそれよりは大きい素数から使って解くことになる 連続でなくともよいなら素数は無限にあるので無限にある 連続素数もおそらくは無限にありそうに思う

…	その画像、wikipediaのを切り貼りしたのか https://ja.wikipedia.org/wiki/%E9%AD%94%E6%96%B9%E9%99%A3