12月28日頃消えます 1=2 の証明スレ
数学好きなら2つや3つくらい目にしてるはず
とりあえず1つめ
1=1+0+0+0+0+…
=1+(1-1)+(1-1)+(1-1)+(1-1)+…
=1+1-1+1-1+1-1+1-1+…
=1+1+(-1+1)+(-1+1)+(-1+1)+(-1+1)+…
=1+1+0+0+0+0+…
=2 削除された記事が1件あります.見る
| … |
b = a とする。この両辺に a を足すと a + b = 2a 両辺から 2b を引くと a - b = 2a - 2b (a - b) = 2(a - b) 両辺を (a - b) で割ると 1 = 2 |
| … |
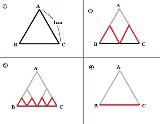 1辺の長さが1cmの正三角形ABCにおいて、 ①AB+AC=2cm、BC=1cmである。②のように、各辺の中点を結ぶと、赤い線分の長さの合計LはAB+AC=2cmに等しい。③同様の操作を繰り返しても、L=2cmが成り立つ。④無限回繰り返すと、赤い線はBCと重なるので、L=1cm。 一方、③よりL=2cmだから、1=2である。 |
| … |
二つ目 ゼロで割っとるがな |
| … |
3つ目は面白いな |
| … |
男が1人 女が1人 2人いたら合体して1つになるのが生物の性 1+1=1 2=1 |
| … |
1≠2と仮定する 両辺に0をかけると 左辺=0 右辺=0となり 0≠0とならない よって仮定が間違っていることになるので 1=2 |
| … |
>No.112695 1辺1の正方形ABCDの△ABCで同様の作業をすると AB+AD=BD 1+1=√2 2=√2 両辺を2乗すると 4=2 両辺2で割って 2=1 |
| … |
Eulerの公式にθ=2πを代入すると e^2iπ =cos2π+isin2π =cos(2π+2π)+isin(2π+2π) =e^4iπ よって e^2iπ=e^4iπ 両辺の自然対数を取って2iπで割ると 1=2 |
| … |
0=0 0×1=0×2 両辺を0×2で割ると 0×1/0×2 =1 1/2=1 分母をはらって 1=2 |
| … |
i=√-1=√(1/-1)=√1/√-1=1/i 両辺i倍して i^2=1 両辺2倍 -2=2 両辺に6を加える 4=8 両辺を4で割る 1=2 |
| … |
4÷3=1あまり1 3÷2=1あまり1 したがって 4÷3=3÷2 両辺に6をかけると 8=9 両辺から7引いて 1=2 |
| … |
>No.112703 これいいな |
| … |
>No.112695 円の面積の求め方も図で書けばこれに近い考え方だよね |
| … |
100万本の髪の毛から1本抜いても違いは無い 100万=99万9999 99万9999本の髪の毛から1本抜いても違いは無い 99万9999=99万9998 99万9998本の髪の毛から1本抜いても違いは無い 99万9998=99万9997 …という作業を繰り返すと最終的に2=1になる |
| … |
1+1+1+1+1+1+1+…= s とする 1+1+1+1+1+1+1+… = 1+1+1+1+1+1+1+… 1+(1+1+1+1+1+1+1+…) =1+1+(1+1+1+1+1+1+1+…) 両辺の(1+1+1+1+1+1+1+…)にsを代入 1+s=1+1+s 1=2 |
| … |
諸兄らが詐欺師にひっかからないように詐欺師の手口に通暁しているのはよくわかった |
| … |
y=0xという関数を考える x=1のときy=0 x=2のときy=0 したがって 1=2 |
| … |
sin(2π/n)=sin(4π/n) n→無限大で 2π/n=sin(2π/n),sin(4π/n)=4π/n よって4π/n=2π/n 両辺n/2倍して 1=2 |
| … |
0か無限大を使うのが定番って感じだね |
| … |
ほんまやな 0の除算ってのも無限大やし |
| … |
無限大を扱う時は慎重に議論しないと1=2みたいな誤謬を導いてしまうことがよく分かる |
| … |
>0か無限大を使うのが定番って感じだね 定番ではなく流行ネタ(すでに廃れ気味だが)を使ってやってみた 2÷√2(√2/2+√2/2)という計算を考える カッコ→左から順番に計算すると 2÷√2(√2/2+√2/2) =2÷√2×√2 =√2×√2 =2 √2とカッコの乗法を優先すると 2÷√2(√2/2+√2/2) =2÷(√2×√2) =2÷2 =1 どちらも2÷√2(√2/2+√2/2)の結果であるから1=2 |
| … |
書き込みをした人によって削除されました |
| … |
f(x,y)=1+x/(x+y)という関数のx,y→∞の極限を考える lim(x→∞)[lim(y→∞) f(x,y)] =lim(x→∞) (1+0) =1 lim(y→∞)[lim(x→∞) f(x,y)] =lim(y→∞) (1+1) =2 以上より、lim(x,y→∞) f(x,y)=1=2 |
| … |
0!=1 1!=1 よって 0=1 両辺に1を加えて 1=2 |
| … |
海に砂粒を一つ落とそうが 二つ落とそうが、 体積の変化は議論にならないってのと同じ 無限になんとかって発想を用いずに証明してみてくれ |
| … |
>No.112791 こんな感じに これは、0!=1 と定義するなら、そうなるだろ、って気は瞬間的にした |
| … |
>No.112791 正直これは f(x)=x^2-1とするとf(1)=f(-1)=0、よって1=-1 って言ってるくらいおかしな議論だけどな |
| … |
3!=2!×3 両辺を!で割って 3=2×3 両辺を3で割って 1=2 |
| … |
>両辺を!で割って !を掛けたらどんな数字になるんだ? |
| … |
>!を掛けたらどんな数字になるんだ? 40−32÷2=4 という間違いの式が 40−32÷2=4! 正しくなる |
| … |
>40−32÷2=4!正しくなる 掛け算する時は両辺に掛けるって教わらなかったのか? |
| … |
>掛け算する時は両辺に掛けるって教わらなかったのか? 40−32÷2=4 80-32=4 80=40 2=1 両辺に!をかけて 2!=1! よって2=1 (ちょっと変形したけど)言われたとおりに両辺にかけてみた |
| … |
>80-32=4 右辺2倍し損ねた 8に訂正お願いします |
| … |
リンゴが1個、ミカンが1個 合わせて2個 リンゴが1個あってリンゴを1個追加しました 合わせて2個 リンゴを半分にしました、2個に増えました 半分のしたリンゴを合体しました リンゴは1個 1=2です |
| … |
アルファベット数が等しい単語であることを表す記号を=とする one=two したがって 1=2 である |
| … |
>アルファベット数が等しい単語であることを表す記号を=とする 記号の定義を変えるのがありなら アルファベット数 を 文字、記号、数字の数 にするだけで 1=2 |
| … |
つまらn |
| … |
すべての整数の中で最大のものを A とおく。一般に、 A + 1 ≧ A A は最大の整数だから、 A ≧ A + 1 ゆえに A = A + 1 両辺から A-1 を引くと 1 = 2 |
| … |
RとR^2の間には全単射が存在する よって1=2 |
| … |
0.999… = 1 両辺に14を足してから10で割ると 1.4999… = 1.5 両辺の小数第一位を四捨五入して整数にすると 1 = 2 |
| … |
まだやってるのかw |