19年8月頃消えます 1からkまでの自然数から重複を許してランダムに二数を選び、それぞれa,bとする。また、k以下の素数の数をpとする。

kまでの自然数が全て同様に1/kの確率で選ばれるとき、b/aおよびa/bの一方もしくは両方が自然数になる確率をk,pで表せ。

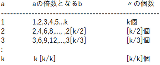…	まずa≦bに限って考える bがaの倍数になる場合の数Dはガウス記号[]を用いてD = k+[k/2]+[k/3]+...+[k/k] (画像参照)a≦bの制約を外した時にa,bが問題の条件を満たす場合の数は 2(D-k)+k = 2D+k なので求める確率はa,bの取りうる場合の数k^2で割ることで (2D+k)/k^2残る問題のD だけどどうやらこれに等しいらしいが…https://en.wikipedia.org/wiki/Divisor_summatory_functionpとkで表示する方法がワカラン

…	最大素数の簡単な見つけ方 ①確認されてる最大の素数と その１個前の素数を掛ける ②それに１足す