戝妛擖帋椙栤僗儗
tan1亱偼桳棟悢偐
乮2006 嫗搒戝妛乯
僔儞僾儖側栤戣偺拞偵
丒tan1偑柍棟悢偱偁傞偲偄偆梊憐傪棫偰傞擻椡
丒婣擺朄偲攚棟朄傪寢傃偮偗傞擻椡
偑栤傢傟偰傞偙偺栤戣杮摉偵岲偒嶍彍偝傟偨婰帠偑2審偁傝傑偡.尒傞
| 乧 |
亂栤戣侾亃tan1亱偑柍棟悢偱偁傞偙偲傪帵偟側偝偄丅 亂栤戣俀亃cos1亱偑柍棟悢偱偁傞偙偲傪帵偟側偝偄丅 亂栤戣俁亃sin1亱偑柍棟悢偱偁傞偙偲傪帵偟側偝偄丅 http://open.mixi.jp/user/14882521/diary/1282208078 |
| 乧 |
惓敧柺懱偺傂偲偮偺柺傪壓偵偟偰悈暯側戜偺忋偵抲偔丅 偙偺敧柺懱傪恀忋偐傜尒偨恾(暯柺恾)傪偐偗丅 (2008擭搶戝棟宯戞3栤) |
| 乧 |
tan兛, tan兝 偑椉曽偲傕桳棟悢偩偲偡傞偲丄 tan(兛+兝) = (tan兛+tan兝)/(1-tan兛tan兝) 傕桳棟悢偵側傞丅 偟偨偑偭偰丄tan兛偑桳棟悢偺偲偒丄 tan2兛=tan(兛+兛)傕桳棟悢丄tan3兛=tan(2兛+兛)傕桳棟悢丄tan5兛=tan(2兛+3兛)傕桳棟悢偵側傞丅 偄傑 tan1亱偑桳棟悢偲壖掕偡傞偲丄 tan2亱傕桳棟悢丄tan10亱傕桳棟悢丄tan20亱傕桳棟悢丄tan60亱傕桳棟悢偵側傞丅 偲偙傠偑 tan60亱=併3 偱柍棟悢偩偐傜丄偙傟偼柕弬偱偁傞丅 偟偨偑偭偰 tan1亱偼桳棟悢偱偼側偄丅 |
| 乧 |
>tan兛偑桳棟悢偺偲偒丄 >tan2兛=tan(兛+兛)傕桳棟悢丄tan3兛=tan(2兛+兛)傕桳棟悢丄>tan5兛=tan(2兛+3兛)傕桳棟悢偵側傞丅 偳偆偟偰? |
| 乧 |
偪傚偭偲徣棯偟偰彂偒偡偓偨偐傕丅 > tan兛, tan兝 偑椉曽偲傕桳棟悢偩偲偡傞偲丄 > tan(兛+兝) = (tan兛+tan兝)/(1-tan兛tan兝) 傕桳棟悢偵側傞丅 偙傟傪乻曗戣乼偲偡傞丅 tan兛偑桳棟悢偺偲偒丄 乻曗戣乼偺兝傪兛偱抲姺偡傞偲tan2兛傕桳棟悢偵側傞丅乧嘆 乻曗戣乼偺兝傪2兛偱抲姺偡傞偲嘆偲崌傢偣偰tan3兛傕桳棟悢偵側傞丅乧嘇 乻曗戣乼偺兛傪2兛偱抲姺偟丄兝傪3兛偱抲姺偡傞偲嘆, 嘇偲崌傢偣偰tan5兛傕桳棟悢偵側傞丅 偙傟偱椙偄偱偟傚偆偐丅 |
| 乧 |
桳棟悢偺巐懃墘嶼偺寢壥偼桳棟悢偵側傞偭偰帺柧偺傛偆偵巊偭偰偄偄傫偩傠偆偐偲偐峫偊弌偡偲夝摎偑偳傫偳傫挿偔側傞 |
| 乧 |
併俁偑柍棟悢側偺傕帺柧偲偟偰埖偭偰偄偄偐偺偐偺傕擸傓 |
| 乧 |
>偪傚偭偲徣棯偟偰彂偒偡偓偨偐傕丅 偁偁偛傔傫丄堦斣忋偺壛朄掕棟尒摝偟偰偨傢 |
| 乧 |
> 桳棟悢偺巐懃墘嶼偺寢壥偼桳棟悢偵側傞偭偰帺柧偺傛偆偵巊偭偰偄偄傫偩傠偆偐偲偐峫偊弌偡偲夝摎偑偳傫偳傫挿偔側傞 > 併俁偑柍棟悢側偺傕帺柧偲偟偰埖偭偰偄偄偐偺偐偺傕擸傓 擖帋偺摎埬側傜偒偪傫偲徹柧偡傞傋偒偐傕抦傟側偄偗偳丄偦偙偼宖帵斅側偺偱嵶偐偄偲偙傠偼偛梕幫婅偄傑偡丅 |
| 乧 |
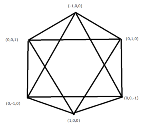 > 惓敧柺懱偺傂偲偮偺柺傪壓偵偟偰悈暯側戜偺忋偵抲偔丅 > 偙偺敧柺懱傪恀忋偐傜尒偨恾(暯柺恾)傪偐偗丅> (2008擭搶戝棟宯戞3栤)偙傫側姶偠偺恾偵側傞偐傕丅惓敧柺懱偵偼柺偑俉屄丄捀揰偑俇屄丄曈偑侾俀屄偁傝丄捀揰偺嵗昗偼(亇1,0,0), (0,亇1,0), (0,0,亇1) 偲昞偡偙偲偑偱偒傞丅 |
| 乧 |
恾偑墭偄偺偼偛梕幫偔偩偝偄丅 杮摉偼偒傟偄側惓榋妏宍偵側傞偼偢偱偡偑忋庤偵昤偗傑偣傫偱偟偨丅 |
| 乧 |
 2017 惞儅儕 1乣3偼掕斣偩偗偳丄4偐傜偑夝偄偰偰妝偟偄 |
| 乧 |
> 2017 惞儅儕 (1) 偼 (i) 偱 a=b=0偲偡傞偲 f(0) = f(0+0) = f(0)+f(0) 偲側傞丅 偙傟傪堏崁偡傞偲 f(0)=0 偵側傞丅 (2) 偼 (ii) 偱 a=b=1偲偡傞偲 f(1) = f(1*1) = f(1)*f(1) 偲側傞丅 (iii) 傛傝 f(1) 偼 0 偱偼側偄偺偱妱傞偙偲偑偱偒傞偐傜 f(1)=1 偲側傞丅 (3) 偼 (i) 偱 a=n-1, b=1偲偡傞偲 f(n) = f((n-1)+1) = f(n-1)+f(1) = f(n-1)+1 偲側傞丅 傑偨丄f(1)=1 偩偐傜婣擺朄傛傝 f(n)=n 偲側傞丅 |
| 乧 |
彂偒崬傒傪偟偨恖偵傛偭偰嶍彍偝傟傑偟偨 |
| 乧 |
(4) 惓偺桳棟悢 q 傪 q=n/m 偲偍偔丅(n, m 偼惓偺惍悢) (ii) 偱 a=n, b=1/m 偲偡傞偲 f(q) = f(n/m) = f(n*(1/m)) = f(n)*f(1/m) 偲側傞丅 f(n)偼暘偐傞偑丄f(1/m)偑暘偐傜側偄偺偱師偺傛偆偵媮傔傞丅 (ii) 偱 a=m, b=1/m 偲偡傞偲 f(1) = f(m*(1/m)) = f(m)*f(1/m) 偲側傞丅 f(1)=1, f(m)=m 偩偐傜 f(1/m)=1/m 偱偁傞丅 埲忋偺偙偲偐傜 f(q) = f(n/m) = f(n*(1/m)) = f(n)*f(1/m) = n*(1/m) = n/m = q 偲側傞丅 |
| 乧 |
彂偒崬傒傪偟偨恖偵傛偭偰嶍彍偝傟傑偟偨 |
| 乧 |
(5) t偼惓偺幚悢偩偐傜丄併t 傕幚悢偱偁傞丅 (ii) 偱 a=併t, b=併t 偲偡傞偲 f(t) = f(併t*併t) = f(併t)*f(併t) = f(併t)^2 亞 0 偲側傞偐傜丄f(t)偼0傑偨偼惓偱偁傞偙偲偑暘偐傞丅 傑偨丄t偼惓偺幚悢偩偐傜丄1/t 傕幚悢偱偁傞丅 (ii) 偱 a=t, b=1/t 偲偡傞偲 f(1) = f(t*(1/t)) = f(t)*f(1/t) 偲側傞丅 堦曽丄f(1)=1 偩偐傜丄f(t)偼0偱偼側偄偙偲偑暘偐傞丅 埲忋偺偙偲偐傜丄f(t)亜0 偱偁傞偲偄偊傞丅 |