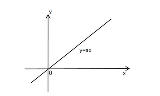
原点を通る直線を適当に引いたとき、その直線が原点以外の格子点を通る確率は？
という問題なのですが、投稿者が回答をインスタのストーリーという形式で上げたため、投稿から24時間以上たった今では回答を見ることができません
どういう答えになりますか？
https://twitter.com/Yobinori/status/1014722323125919744削除された記事が2件あります.見る

…	格子密度は？何も書かれていなかったら整数倍格子が常識なの？

…	直線ってことは太さ0だから限りなく確率0に近いような

…

本文ない

…

なぜその画像を？

…	有理数濃度/実数濃度だから0でよさそうね

…	>なぜその画像を？ 太さがゼロって流れだからじゃない？

…	書き込みをした人によって削除されました

…	書き込みをした人によって削除されました

…	>No.109592 ぶっちゃけ、0 なのですよ。理由としては、可算無限集合はルベーグ測度に関して零集合であることによるからなのですよ。補足すれば、デカルト座標系上の座標点全体の集合が非可算集合である一方で、格子点全体の集合が可算無限集合だからなのですよ。>No.109598ぶっちゃけ、「どっちが近い」かどうかは「斜め」の経路が弧長 2 の測度を有しているかどうかに依存するのですよ（設問がill-posed）。余談なのですが、「悪魔の階段」（絶対連続ではない連続写像）は弧長 2 なのですよ。

…	批判はするが正解は示さないクズ

…	>ぶっちゃけ、0 なのですよ。 久々のぶっちゃけさんだ この場合の確率は0として、 逆に直線に少しでも太さがある場合だと確率は1になるの?

…	>No.109616 ぶっちゃけ、（ユークリッド平面におけるデカルト座標系を前提とすれば）原点を内包する「幅に測度を有する平行線に挟まれた帯」（太さのある「直線」）であれば、原点以外の格子点を通る確率は 1 になるのですよ。というのも、そもそも格子点を通る必要十分条件としては、帯の通る座標点 (x,y) が一つでも、x と y の値がともに有理数であることが示されればいいのですが、有理数の稠密性より、任意の実数 r,s（但しr<s） の開区間には必ず r<q<s となる有理数 q が存在するため、x と y がともに有理数である座標点 (x,y) を通らざるを得ないからなのですよ。

…

キモッ　オエッ

…	>悪魔の階段 クロネッカーがアップを始めました

…	適当に引く、がill-defined つか適当に引いた直線が半直線(1, 0)-(1, 1)と 座標(1, y)において交叉したとき yが有理数である確率を考えたらﾜｶﾙ

…	>適当に引く、がill-defined ここでは恣意的な操作を介さないという意味で 偏角がランダム（一様分布）であるという解釈で いいかと思われ

…	ウェルディファインドをそんなつもりで使ってる例を俺は知らないんだけど？

…	離散一様分布ならまだ勝ち目はある

…	>ウェルディファインドをそんなつもりで使ってる例を俺は知らないんだけど？ つ[ビュフォンの針]

…

掛け谷の問題の方が

…	ぶっちゃけの貼る画像が気持ち悪い 好きな奴が擁護してるのも気持ち悪いっおえ

…	キチガイにかまうな。黙ってDel

…	サイエンス社刊数理科学2017年10月号特集確率論の力の最初の特集記事で具体的な確率分布の選び方に依らないよう理論をつくる「べき」だという意味でウェルディファインド使ってるね

…	ま、ここの規約・マナーではあれぐらいは別に構わないんだけどな。 そもそもそういうことが許される掲示板だし。 画像をご褒美と思ってみてるのはほとんどいないよ。 レス本文が正しいのかどうかにしか関心がない。 ただ、もう話題が似たり寄ったりの低級なのしかでてこなくて、ぶっちゃけのレスも定形文に近くなってるけどな。 ただ、スカトロとグロはエグいのはだめだそうだ。